4. Resolución de áreas en figuras compuestas

Vamos a realizar algunos ejemplos o ejercicios de figuras compuestas. La primera que vamos a realizar es la siguiente, en la cual, cada cuadrícula vale un metro, y lo que tenemos que hacer es calcular el área total de la figura. 

Para calcular el área de una figura compuesta, lo mejor es ir calculando el área de cada una de los polígonos que componen la figura. Los polígonos son: el triángulo ocre, el trapecio rojo, el rectángulo fucsia y el semicirculo azul.

Calculamos primero el área del triángulo ocre, de base 2 m y altura 3 m: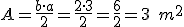

Ahora del trapecio rojo, de base mayor 3 m, base menor 2 m y altura 1 m:

Vayamos con el rectángulo fucsia, de lados 3 y 2 m: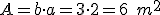

Y por último con la semicircunferencia de radio 1. Calculamos el área de circulo, y lo dividimos por 2:

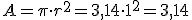; y dividimos por 2;

En total: A = 3 + 2,5 + 6 + 1,57 = 13,07 m²

Y ahora un poco más difícil, porque en la siguiente figura no tienes señaladas las figuras que la componen, debes averiguarlo tú. Calcula en tu cuaderno el área de la figura suponiendo que cada cuadrícula vale 5 cm, y después mira la solución que te proponemos.

 

Los polígonos que componen la figura son: un triángulo, un trapecio y un semicirculo.

Calculamos primero el área del triángulo: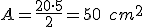

Ahora la del trapecio: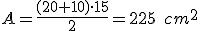

Y la del semicirculo: ; dividiendo por 2: 39,25 cm²

Y sumando todos los datos: 314,25 cm²

Vamos a realizar algunos ejercicios de figuras compuestas.

La primera figura de la que vamos a calcular su área es la siguiente:

Para calcular su área, vamos a ir paso a paso, calculando las áreas de las tres figuras que la componen, el rombo azul, el triángulo rojo y el trapecio verde.

Vamos primero con el rombo azul. El problema es que para obtener el área del rombo necesitamos el valor de sus diagonales, y sólo tenemos el valor del lado, tendremos que buscarnos la vida para calcular las diagonales:

Si miramos el dibujo con atención, vemos que el trapecio verde tiene un lado de longitud 2 cm, que coincide con la mitad de la diagonal mayor del rombo, con lo cual, la diagonal mayor será D = 4 cm. Pero para calcular la diagonal menor, no tenemos ninguna referencia buena. Vamos a representarlo para aclararnos un poco:

Si nos fijamos tenemos cuatro triángulos dentro del rombo. Vamos a tomar el primero de arriba a la derecha, que tendrá las siguientes medidas:
la hipotenusa mide: 2,24 cm; un cateto mide 2 cm (que es la mitad de D, la diagonal mayor), y el otro cateto mide x, que será la mitad de d, la diagonal menor del rombo.

Aplicando el Teorema de Pitágoras, tenemos:

;

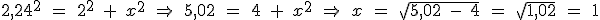así la diagonal menor d, vale 2 cm aproximadamente.

Ahora calculamos el área: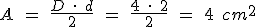

 

 

Ahora calculamos el área del trapecio verde. Para ello necesitamos, tres medidas, que son, la base mayor, la base menor y la altura. Tenemos la altura, 2 cm, tenemos la base menor, 2 cm, pero nos falta la base mayor. Eso sí, si prestamos atención, vemos que tiene que medir 3m, que son la suma de la base menor y la mitad de la diagonal menor del rombo, que era 1 cm, como acabamos de calcular. Así tenemos: B = 3 cm; b = 2 cm; a = 2 cm; y por tanto su área será:

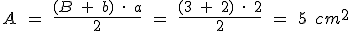
Y por último vamos con el triángulo, cuya base vale 2 cm, como se ve en la figura, y cuya altura, si nos fijamos bien, coincide con la mitad de la diagonal mayor del rombo, por tanto 2 cm. Así el área de triángulo será:

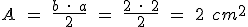
Sumando las tres áreas calculadas, el área total de la figura es: A = 4 + 5 + 2 = 11 cm²