2. Área de polígonos. Teorema de Pitágoras
Ahora vamos a ver cómo se calcula el área de un polígono. Iremos paso a paso, empezando por el área de un cuadrilatero, de un triángulo, y de un polígono en general. Verás lo sencillo que es. Se trata de saber como se llama cada elemento, que ya lo sabemos, y cambiar su valor en la formula que te vamos a dar.
Si quisiéramos explicarle a alguien ¿qué es eso del área? lo mejor sería decirle que es lo que mide una figura, un polígono, o un trozo de tierra que tenemos delante.
Si medimos, por ejemplo la longitud de un lápiz, ésta será de unos 15 centímetros, o si medimos la altura de un edificio obtendremos unos 45 metros, o si medimos la distancia o longitud entre dos ciudades, tendremos por ejemplo que son 225 kilómetros; y es que la longitudes se miden en km, m o cm. Sin embargo, para medir el área de un terreno, diremos que es 100 m2. Esa es la medida de una casa, que sabemos cómo es de grande en función de los metros cuadrados que tenga.
 |
|
http://vivienda-industria-comercio-agricola.blogspot.com/ bajo licencia de creative commons |
Antes de empezar con el cálculo de área, vamos a recordar, el que tal vez sea, el resultado matemático más conocido por la humanidad:
El Teorema de Pitágoras
Este teorema es una fórmula matemática que nos sirve para calcular un lado de un triángulo conociendo los otros dos, pero ¡cuidado! sólo se puede aplicar a una clase de triángulos: los triángulos rectángulos.
Estos triángulos son tan especiales que sus lados tienen nombre propio. Observa la figura:
- Catetos se llaman a los lados que forman el ángulo recto.
- Hipotenusa se llama al lado que está frente al ángulo recto y que, por cierto, siempre es más largo.
El teorema de Pitágoras dice así:
| "En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos". |
Vamos a entenderla, para que nos resulte más familiar.
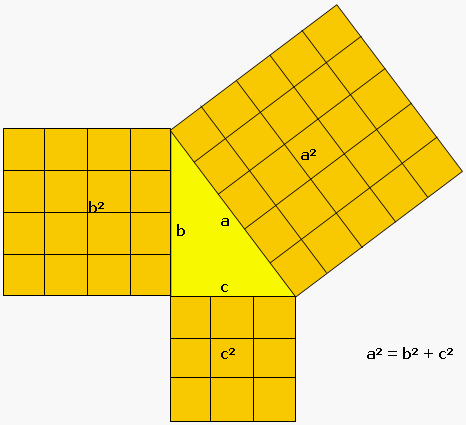
Pues si hacemos por un lado el cuadrado del lado a, la hipotenusa, y por otro los cuadrados de los catetos b y c, y sumamos estos cuadrados de los catetos, obtenemos el mismo resultado. Ya verás:
Como ves, el cuadrado de la hipotenusa, es el mismo número que si sumamos los cuadrados de los catetos. Eso, se escribe, utilizando una fórmula, de la siguiente manera:
a2 = b2 + c2; donde a es la hipotenusa, b y c los catetos.
Veamos un ejemplo de cómo utilizar el Teorema de Pitágoras.
Fíjate en el siguiente gráfico:
Como ves tenemos, un pájaro (échale imaginación, es el circulo amarillo) encima de un árbol (al que también hay que echarle imaginación), y que está a una distancia de un plato con comida representado por el rombo azul. Nos dan lo que vale la altura del árbol, y la distancia desde el árbol hasta el plato. Y nos preguntan a qué distancia está el pájaro del plato. Al representarlo, hemos tenido cuidado para que se vea un triángulo rectángulo, cuya hipotenusa es la distancia que nos piden, y los catetos son las distancias que ya conocemos. Ahora, aplicando la fórmula del Teorema de Pitágoras, y utilizando la calculadora, verás que fácil nos sale:
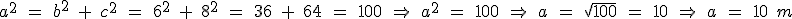
Caso de estudio
 |
|
http://www.monografias.com |
| |
|
Bajo licencia de ccreative commons |