2.1.4 Área de trapecio

Actividad

La fórmula para obtener el área de un trapecio es:

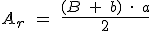; donde B es la base mayor, b es la base menor del trapecio, y a es la altura del mismo


fuente propia	fuente propia

Como vemos los dos trapecios son distintos. El de la derecha es igual a la derecha que a la izquierda. Cuando eso ocurre le llamamos trapecio isósceles. Al de la izquierda, que es distinto a la derecha y a la izquierda, se llama trapecio rectángular.

Vamos a realizar algún ejemplo para aclararnos un poco con esta fórmula.

Por ejemplo, si tenemos que calcular el área y el perímetro del siguiente trapecio rectangular.

trapecio

Lo que hacemos es calcular primero su perímetro. Para ello sumamos las longitudes de sus lados, que son: 11, 6, 8 y 7 m. El lado de la derecha es igual a la altura, por tanto, mide 6 m.

El perímetro será: P = 11 + 6 + 8 + 7 = 32 m

Y ahora calculamos el área del trapecio. Aplicando la fórmula:

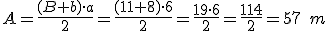
Caso de estudio

Vamos ahora con un ejemplo más concreto. Estamos haciendo una máqueta de una casa de campo. El tejado tiene cuatro partes iguales, y una quinta parte superior que es la que tapa la casa. La parte frontal del tejado, que es igual a las laterales y traseras, es tal como muestra el gráfico siguiente. Y lo que queremos es saber el área total de las 5 piezas, y el perímetro de cada una de las piezas.

trapecio