3.1 Composición de funciones
Muchas funciones habituales pertenecen a la clase de las funciones elementales. Se llaman así porque pueden obtenerse a partir de ciertos tipos de funciones bien conocidas realizando las operaciones de suma, producto, cociente y composición de funciones.
En la siguiente tabla puedes ver cuáles son las principales operaciones con funciones, y cómo afectan estas operaciones a su dominio:
Vamos a prestar especial atención a la composición de funciones, ya que es la única operación desconocida.
Podríamos decir que todo el proceso se compone de tres acciones distintas que se aplican de forma secuencial y ordenada a cada uno de las prendas: Primero lavar, luego secar y por último, planchar. Es fácil, ¿no?
Observa que es importante el orden en que ejecutemos las acciones.
Vamos a componer dos funciones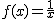 
y 
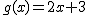. En este caso solo vamos a dar dos pasos: 
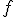sería lavar y 
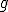secar. Y los números sobre los que se aplican, las prendas.
Por ejemplo, vamos a componer 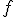y 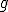sobre el número 2: 
.
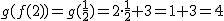Hagamos ahora lo mismo sobre 5: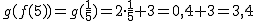 
.
Lavar y secar con 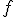y 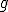el número 2 da como resultado 4, es decir 
. En tanto que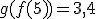 
.
Importante
Dadas dos funciones, 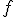y 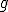, se llama función compuesta de 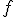con 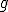a la función: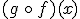 
que se construye del siguiente modo: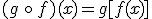 
La expresión 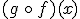la leemos como 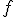compuesta con 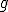de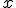 
. Para nombrarla comenzamos por la función que se encuentra a la derecha, más cerca de la 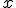, porque es la primera que actúa sobre esta variable.
En la escena siguiente, creada por la profesora Patricia Pérez con GeoGebra, se ilustra con más claridad lo que significa componer dos funciones:
Caso práctico
¿Qué ocurrirá si "lavamos y secamos" los números 4 y 8? O, mejor dicho, calcula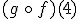 
y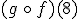 
Apliquemos la composición ahora a un número cualquiera 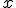, es decir lavemos y sequemos cualquier prenda.
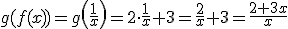
Por tanto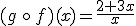 
.
Seguro que lo estás pensando, ¿es lo mismo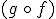 
que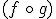 
? Te puedes contestar tú mismo: ¿da igual lavar y secar una prenda que secar y lavarla?, ¿el resultado sería el mismo? Evidentemente, no. Se dice que la composición de funciones no es conmutativa.
Importante
La composición de funciones no es conmutativa
Ejemplo:
Vídeo de las matemáticas.es alojado en Youtube
Caso práctico
Si tenemos las funciones,
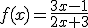
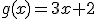
Vamos a calcular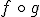 
y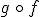 
Caso práctico
Un concesionario oficial de coches ofrece un descuento a los jóvenes menores de 30 años que adquieran un vehículo en sus dependencias. El importe de dicha ayuda está supeditado a los ingresos del comprador.
La ayuda está dividida en tramos. Los tramos vienen definidos por la siguiente función.
Una vez conocido el tramo, la cuantía de la ayuda se obtiene dividiendo 800 euros entre el número de tramo, es decir, si 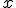es el tramo, la ayuda será:
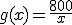
Determina la función a trozos que nos da directamente la cuantía de la ayuda, conocido el sueldo de la persona.
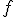y 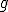, es decir .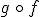