1.3. Relaciones trigonométrics fundamentales

Actividad
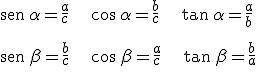
\begin{verbatim}sen\end{verbatim}\, \alpha = \frac{a}{c} \hspace{20} cos \, \alpha = \frac{b}{c} \hspace{20} \begin{verbatim}tan\end{verbatim}\, \alpha = \frac{a}{b} \\ \vspace{5} \\ \begin{verbatim}sen\end{verbatim}\, \beta = \frac{b}{c} \hspace{20} cos \, \beta = \frac{a}{c} \hspace{20} \begin{verbatim}tan\end{verbatim}\, \beta = \frac{b}{a}\\ \vspace{1}
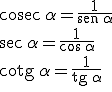
\begin{verbatim}cosec\end{verbatim}\, \alpha = \frac{1}{\begin{verbatim}sen\end{verbatim} \,\alpha} \\ \begin{verbatim}sec\end{verbatim}\, \alpha = \frac{1}{cos \, \alpha} \\ \begin{verbatim}cotg\end{verbatim} \, \alpha = \frac{1}{\begin{verbatim}tg\end{verbatim} \,\alpha} \\ \vspace{1}

Actividad

De las expresiones anteriores podemos dedudir

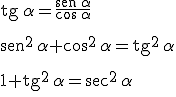
\begin{verbatim}tg\end{verbatim}\, \alpha = \frac{\begin{verbatim}sen\end{verbatim}\, \alpha}{\cos \, \alpha}\\ \vspace{5} \\ \begin{verbatim}sen\end{verbatim}^2\, \alpha+\cos^2 \, \alpha = \begin{verbatim}tg\end{verbatim}^2 \, \alpha\\ \vspace{5} \\ 1+ \begin{verbatim}tg\end{verbatim}^2 \, \alpha= \begin{verbatim}sec\end{verbatim}^2 \, \alpha \\ \vspace{1}

Actividad

\begin{array}{lll} \begin{verbatim}sen\end{verbatim} \,45^\circ = \frac{\sqrt{2}}{2} \hspace{20} & cos \, 45^\circ = \frac{\sqrt{2}}{2} \hspace{20} & \begin{verbatim}tg\end{verbatim} \, 45^\circ = 1 \\ \vspace{5} \\ \begin{verbatim}sen\end{verbatim}\, 30^\circ = \frac{1}{2} \hspace{20} & cos \,30^\circ = \frac{\sqrt{3}}{2} \hspace{20} & \begin{verbatim}tg\end{verbatim} \, 30^{\circ} = \frac{\sqrt {3}}{3} \\ \vspace{5} \\ \begin{verbatim}sen\end{verbatim} \,60^\circ = \frac{\sqrt {3}}{2} & \cos \,60^\circ = \frac{1}{2} & \begin{verbatim}tg\end{verbatim}\, 60^\circ = \sqrt {3} \end{array} \\ \vspace{1}

Actividad

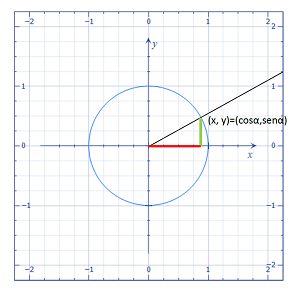
La circunferencia goniométrica es la circunferencia con centro el origen de coordenadas y radio 1.

De esta forma cuando trazamos un ángulo cualquiera tomando como referencia el semieje positivo OX, tenemos que las coordenadas del punto de intersección de la semirrecta que determina el ángulo y la circunferencia goniométrica coinciden con las razones coseno y seno de dicho ángulo, como bien se ve en el dibujo.

Con la circunferencia goniométrica vamos a extender las razones trigonométricas a todos los ángulos entre 0º y 360º. Teniendo en cuenta en esto y que 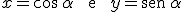x=\cos \, \alpha \ \begin{verbatim} e \end{verbatim} \ y=\begin{verbatim}sen\end{verbatim} \, \alpha podemos deducir

  • Cualquier ángulo del primer cuadrante, es decir, 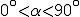0^\circ<\alpha<90^\circ tiene seno, coseno y tangente positivos.

  • Cualquier ángulo del segundo cuadrante, es decir, 90^\circ<\beta<180^\circ tiene seno positivo; y coseno y tangente negativos.

  • Cualquier ángulo del tercer cuadrante, es decir, 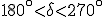180^\circ<\delta<270^\circ tiene seno y coseno negativos; y tangente positiva.

  • Cualquier ángulo del cuarto cuadrante, es decir, 270^\circ< heta<360^\circ tiene seno y tangente negativos; y coseno positivo.

Una vez que sabemos cómo calcular las razones trigonométricas de cualquier cuadrante a partir de las razones de un ángulo del primero, podemos calcular las razones de un ángulo cualquiera. Si ese ángulo es mayor de 360º sólo tenemos que dar vueltas en el sentido contrario a las agujas del reloj para determinarlo.

 

Ejemplo

Si queremos determinar las razones trigonométricas de 855º:

Si dividimos 855º entre 360º da de cociente 2 y de resto 135º. Esto significa que para llegar a 855º tenemos que dar dos vueltas completas y 135º más por lo que las razones de 855º coinciden con las razones del resto de la división, es decir, con las razones de 135º. 

Si las razones que queremos determinar son de un ángulo negativo, por ejemplo -1290º:

Las vueltas ahora las damos al revés, es decir, en el sentido de las agujas del reloj. Si dividimos 1290º entre 360º queda como cociente 3 y resto 210º. Por tanto para llegar a -1290 tenemos que dar 3 vueltas completas y 210º más en el sentido de las agujas del reloj, esto quiere decir que las razones trigonométricas de -1290º coinciden con las de -210º, pero -210º = 0º - 210º Ξ 360º - 210º = 150º (donde Ξ significa que ambas expresiones son equivalentes porque las razones de 0º coinciden con las de 360º ya que sólo se diferencian en una vuelta).

En conclusión las razones de -1290º coinciden con las razones de 150º

Actividad

Dados dos ángulos cualesquiera α y β se tiene que:

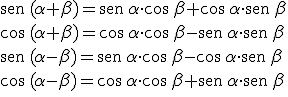\begin{verbatim}sen\end{verbatim} \, (\alpha +\beta) = \begin{verbatim}sen\end{verbatim} \, \alpha \cdot \cos \, \beta + \cos \, \alpha \cdot \begin{verbatim}sen\end{verbatim} \, \beta \\ \cos \, (\alpha +\beta) = \cos \, \alpha \cdot \cos \, \beta - \begin{verbatim}sen\end{verbatim} \, \alpha \cdot \begin{verbatim}sen\end{verbatim} \, \beta \\ \begin{verbatim}sen\end{verbatim} \, (\alpha -\beta) = \begin{verbatim}sen\end{verbatim} \, \alpha \cdot \cos \, \beta - \cos \, \alpha \cdot \begin{verbatim}sen\end{verbatim} \, \beta \\ \cos \, (\alpha -\beta) = \cos \, \alpha \cdot \cos \, \beta + \begin{verbatim}sen\end{verbatim} \, \alpha \cdot \begin{verbatim}sen\end{verbatim} \, \beta \\ \vspace{1}