5.- Especial Selectividad
Ejemplo o ejercicio resuelto
¿Son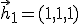 
, 
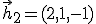y 
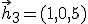una base de 
?
Si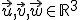 
son linealmente independientes, ¿forman los vectores 
, 
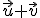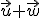y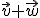 
una base de ?
AV - Reflexión
En , sean los vectores
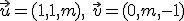y 
a)¿Para qué valores de m son linealmente dependientes?
b)Determinar en tal caso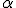 
y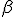 
de modo que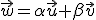 
Ejemplo o ejercicio resuelto
Demuestra que si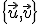 
es una base de 
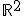entonces 
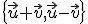también es una base.
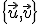es una base de 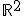entonces 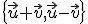también es una base.
Ejemplo o ejercicio resuelto
a) Determinar un valor de p para que los vectores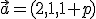 
, 
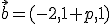y 
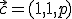sean linealmente dependientes.
b) Para el valor de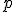
obtenido, hallar una relación de dependencia lineal entre esos vectores.
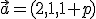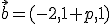, y 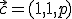sean linealmente dependientes.b) Para el valor de
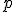obtenido, hallar una relación de dependencia lineal entre esos vectores.
AV - Reflexión
Determina un vector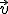 
de sabiendo que cumple las tres siguientes condiciones:
1.- La suma de sus tres coordenadas es 3.
2.- 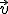es combinación lineal de 
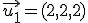y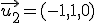 
3.- Los vectores (1,0,1), (0,1,0) y 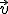son linealmente dependientes
Ejemplo o ejercicio resuelto
Dados los puntos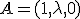 
, 
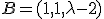y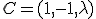 
Comprueba que no está alineados cualquiera que sea el valor de 
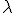y calcula el perímetro del triángulo que forman
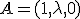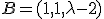, y 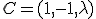Comprueba que no está alineados cualquiera que sea el valor de 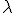y calcula el perímetro del triángulo que forman
AV - Reflexión
Hallar el valor de "k" para que los puntos A, B, C y D estén en el mismo plano, siendo A=(2,-1,2), B=(4,-3,-1), C=(-2,1,1) y D=(-1,-1,k)
AV - Reflexión
Dados los puntos A=(λ,2,λ), B=(2,-λ,0) y C=(λ,0,λ+2):
a) ¿Para qué valores de λ están los tres puntos alineados?
b) Comprueba que cuando los puntos no estén alineados, entonces el triángulo formado por A, B y C es isósceles.