4.- Distancia entre dos puntos
 |
| Estantería. Imagen del ITE |
Importante
Intentamos ahora calcular la distancia entre dos puntos del espacio. Para ello vamos a utilizar la pantalla interactiva que aparece debajo de este texto. Partimos de dos puntos del espacio 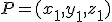 y
y 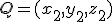 . Para calcular la distancia entre estos dos puntos, observamos en la escena inferior que los puntos
. Para calcular la distancia entre estos dos puntos, observamos en la escena inferior que los puntos 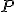 ,
, 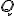 y
y 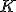 forman un triángulo rectángulo, por tanto
forman un triángulo rectángulo, por tanto
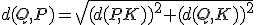
Pero según observamos en la imagen
![]()
También observamos en la imagen que
![]()
Por el teorema de Pitágoras
![]()
Por tanto
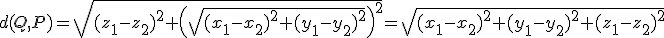
En la escena de abajo puedes ver la distancia entre dos puntos P y Q. Si mueves estos puntos puedes ver como varía la distancia entre los mismos. Siempre puedes reiniciar la escena pulsando en el icono de la parte superior derecha, así como verla desde distintos puntos de vista moviendo el ratón sobre ella con el botón izquierdo pulsado.
Por si te puede servir te dejamos esta ventana en la que podrás calcular la distancia entre dos puntos del espacio:
Ejemplo o ejercicio resuelto
En muchas de las animaciones gráficas que se realizan para juegos y gráficos, necesitamos calcular la distancia entre puntos característicos del objeto que estemos dibujando. En este caso vamos a plantearnos calcular distintas medidas en un objeto que vamos a utilizar más adelante. El objeto es un cubo y lo hemos representado en la ventana interactiva que observas más abajo. Los vértices del cubo tienen por coordenadas A=(5,5,6), B=(5,5,2), C=(5,1,2), D=(5,1,6), E=(1,5,6), F=(1,5,2), G=(1,1,2) y H=(1,1,6)
Necesitamos que calcules las siguientes distancias:
1.- d(A,B)
2.- d(A,H)
3.- d(A,C)
4.- d(A,G)
5.- Necesitamos calcular también el punto medio del cubo.
Ejemplo o ejercicio resuelto
El pulpo tiene 8 patas como observamos en la fotografía.
 |
| Pulpo. Imagen obtenida del ITE |
Para conseguir situar las ocho patas del pulpo se ha partido de un cuadrado sobre el que se ha situado otro cuadrado girado, consiguiendo los ocho puntos tal y como se observa en la imagen animada. El cuadrado primero tiene por vértices A, B, C y D. Los puntos de corte de los dos cuadrados determinan un octógono sobre el que se va a distribuir las patas del pulpo.
Observa en la imagen animada la forma en la que se obtienen los distintos vértices del octógono:
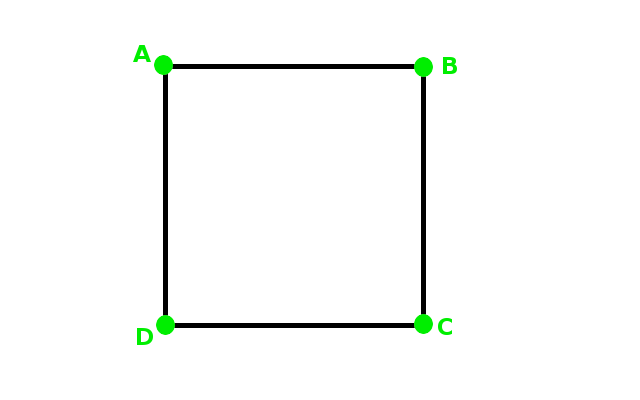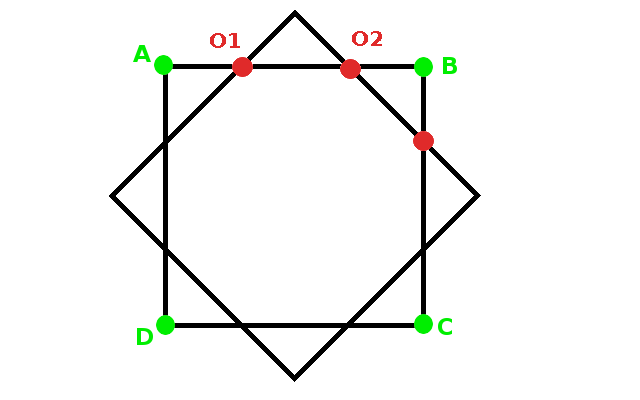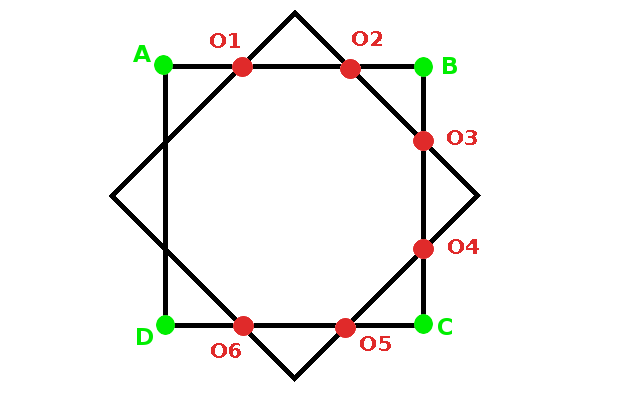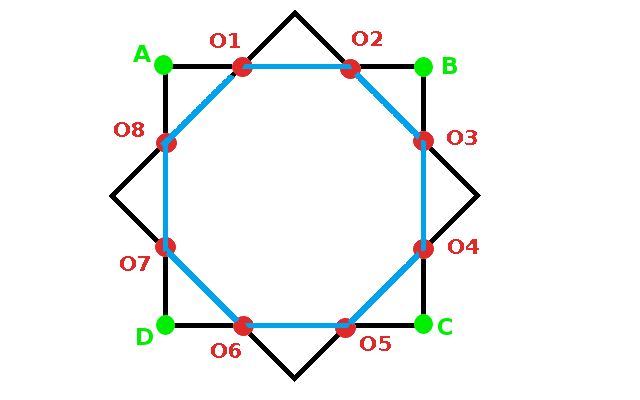 |
Como puedes observar es una imagen que guarda bastantes simetrías que podemos utilizar para la resolución del ejercicio que nos van a plantear. De este octógono nos proporcionan los vértices A=(-5,7,4), B=(5,7,4) y D=(-5,7,-6). Para resolver el ejercicio que planteamos de cara al futuro diseño debemos:
1.- ¿Son A, B y D vértices de un cuadrado?
2.- En caso de serlo, calcula el vértice C.
3.- Si la distancia que hay de A al vértice O1 es 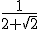 la distancia que hay de A a B, Calcula los vértices del octógono.
la distancia que hay de A a B, Calcula los vértices del octógono.
AV - Reflexión
Sean los vectores (1,0,0) y (1,1,0).
Probar que son linealmente independientes.
Encontrar un vector 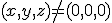 que sea combinación lineal de los anteriores y perpendicular a (1,0,0)
que sea combinación lineal de los anteriores y perpendicular a (1,0,0)