3.1 Puntos en el espacio afín

¿Recuerdas como se dibujaban las coordenadas de un punto en el plano? Haz memoria en la siguiente pantalla:

Coordenadas de un punto
Vídeo alojado en Youtube

Pero ahora nos encontramos en el espacio de tres dimensiones y, por tanto, partimos de tres ejes:

   

   

Imágenes de elaboración propia

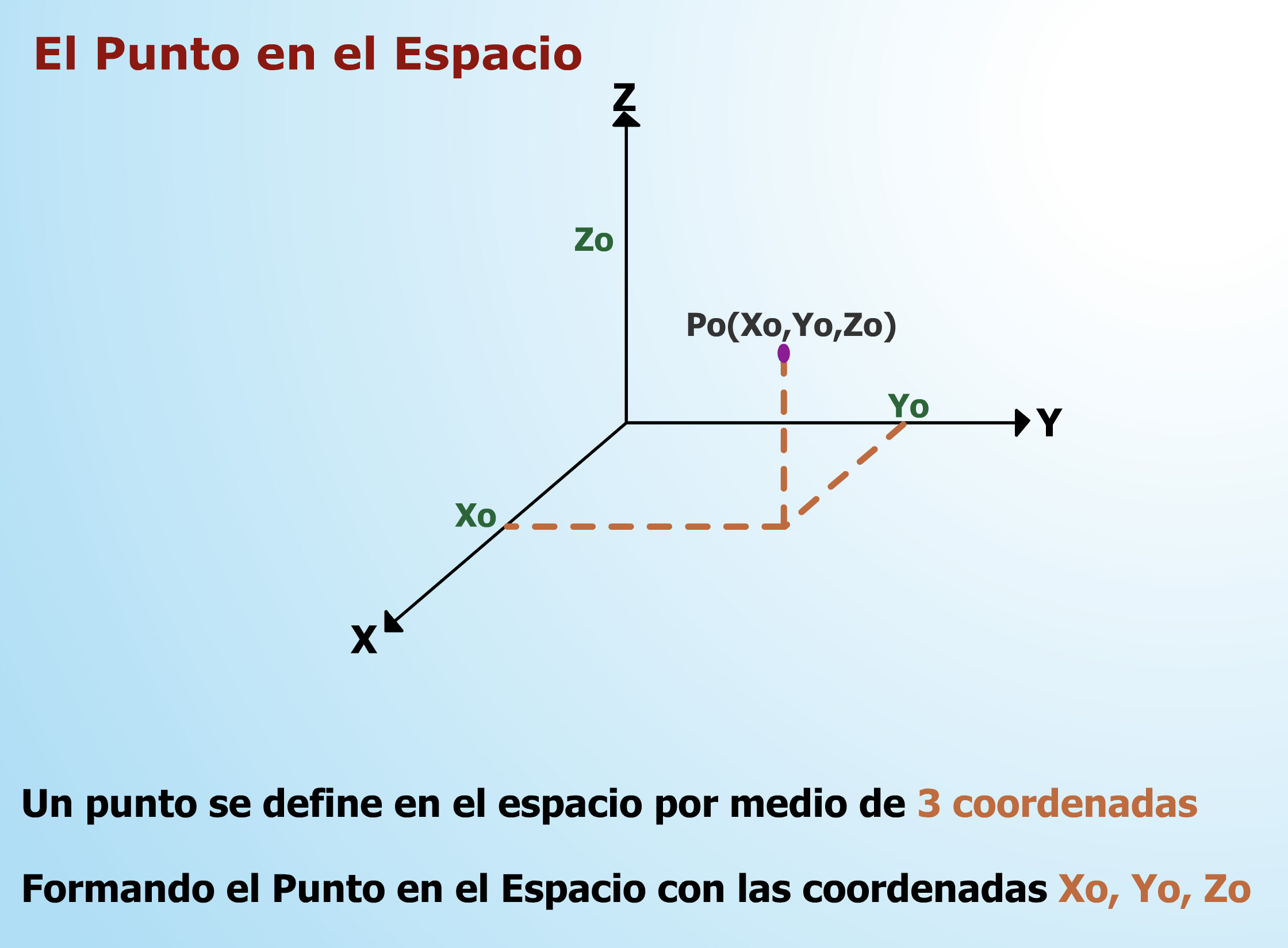
MOVEMOS UN PUNTO SEGÚN LO QUE NOS MARCA UN VECTOR: Para mover un punto P=(p1,p2,p3) según lo que nos marca un vector de coordenadas (v1,v2,v3) el resultado es otro punto Q=P+v=(p1, p2, p3)+(v1,v2,v3) = (p1+v1,p2+v2,p3v3)

En la escena de abajo puedes observar el resultado de trasladar un punto P según lo que le marca un vector v.

Applet alojado en GeoGebra. Licencia CC

AV - Actividad de Espacios en Blanco

Calcula el punto Q que resulta de trasladar el punto P según lo que le marca el vector de cada apartado.

1.- P=(1,-1,2) trasladado por el vector (-1,2,0)

2.- P=(1,0,3) trasladado por el vector (-1,1,-1)

3.- P=(4,3,2) trasladado por el vector (2,-2,3)

4.- P=(5,-1,1) trasladado por el vector (-1,1,3)

1.- Q=

2.- Q=

3.- Q=

4.- Q=

Enable JavaScript

Ejemplo o ejercicio resuelto

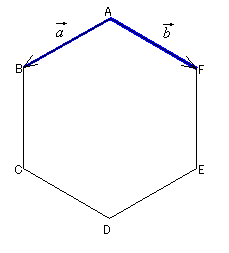Dado un Hexágono regular como el que aparece en la imagen, si conocemos el vértice A y los vectores 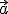y 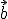, ¿cómo podríamos determinar el resto de los vértices? Para que te resulte más fácil te proporcionamos más abajo una ventana interactiva sobre la que podrás obtener otros vectores que te pueden resultar útiles.

Basta que al final de la ventana elijas el vector que quieres saber cuánto vale y pulses Back o Next.