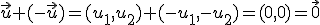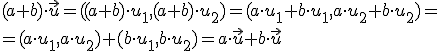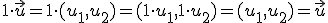1.3 Concepto de espacio vectorial
Importante
|
Definición de espacio vectorial. Mariano Real.
Vídeo alojado en Youtube
Como te ha indicado Descartes, ya conoces dos espacios vectoriales sobre los que has estado trabajando, el plano 1.- Si x e y son dos elementos del conjunto V, entonces x+y=y+x. 2.- Si x, z e y son tres elementos del conjunto V, entonces (x+y)+z=x+(y+z). 3.- Existe un elemento del conjunto V que representaremos por 0 de forma que 0+x=x para todos los elemntos x del conjunto V. Lo llamaremos elemento neutro. 4.- Si x es un elemento del conjunto V existe otro elemento que representaremos por -x de forma que x+(-x)=0 para todos los elementos x del conjunto V. 5.- Si k es un número y x e y son elementos del conjunto V, entonces k·(x+y)=k·x+k·y . 6.- Si k y p son números, entonces k·(p·x)=p·(k·x) para todos los elementos x del conjunto V. 7.- Si k y p son números, entonces (k+p)·x=(k·x)+(p·x) para todos los elementos x del conjunto V. 8.- 1·x=x para todos los elementos x del conjunto V. Así, en el conjunto de todos los vectores del plano, 1.- 2.-
3.-El elemento neutro es 4.- Dado 5.- que es un vector de 6.- 7.- 8.- Esto mismo sucede en el espacio de tres dimensiones Es una definición demasiado teórica, por lo que vemos a verla con algunos ejemplos: |
Ejemplo o ejercicio resuelto
Si consideramos el conjunto de todos los vectores del espacio  que tienen la forma
que tienen la forma 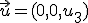 , es decir, que las dos primeras coordenadas son cero, vamos a ver si este conjunto con la operación suma de vectores y la operación del producto de un número por un vector, que ya conocemos, es un espacio vectorial.
, es decir, que las dos primeras coordenadas son cero, vamos a ver si este conjunto con la operación suma de vectores y la operación del producto de un número por un vector, que ya conocemos, es un espacio vectorial.
Ejemplo o ejercicio resuelto
Si consideramos el conjunto de todos los vectores del espacio  y definimos el producto de un número por un vector como
y definimos el producto de un número por un vector como
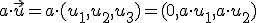
vamos a ver si este conjunto con la operación suma de vectores y la operación del producto de un número por un vector definida, es un espacio vectorial.
Para saber más
El concepto de espacio vectorial se puede aplicar a múltiples conjuntos en matemáticas. Te proponemos que compruebes los dos siguientes puntos:
1.- El conjunto formado por el espacio 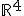 cuyos vectores tienen la forma
cuyos vectores tienen la forma  con la operación suma de vectores que conoces y te recordamos abajo, y el producto de un número por un vector que te recordamos, es un espacio vectorial:
con la operación suma de vectores que conoces y te recordamos abajo, y el producto de un número por un vector que te recordamos, es un espacio vectorial:
1.1 Suma de vectores 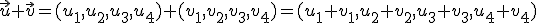
1.2 Producto de un número por un vector 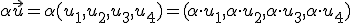
2.- El conjunto formado por las matrices de orden 3x3 con la operación suma de matrices y producto de un número por un matriz es un espacio vectorial
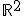 y el espacio
y el espacio 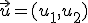 ,
, 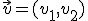 y
y  y los números
y los números  y
y 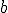 , entonces:
, entonces: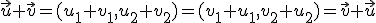 .
.
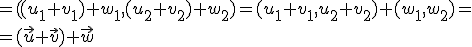
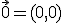 , ya que
, ya que 
 ya que
ya que