1.1 Vectores en el plano
¿Recuerdas qué era un vector y cómo calcularlo? Bueno, vamos a refrescar un poco la memoria. Mira a tu alrededor y céntrate en un objeto.
 |
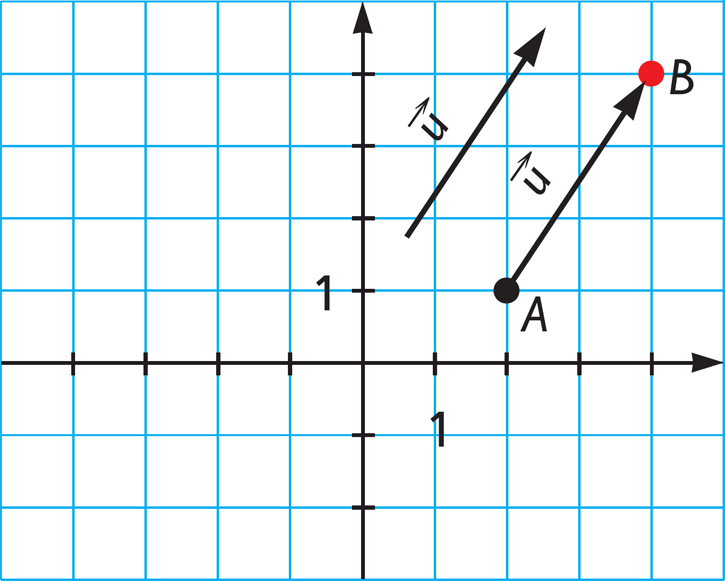Si quisieras arrastrarlo aplicándole una fuerza, esa fuerza será de una determinada medida, se la aplicarás en una dirección concreta y se la aplicarás tirando o empujando. Si ese vector de fuerza es el que va desde el punto del plano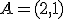
al punto 
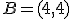, entonces ese vector es 
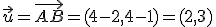. Este vector lo observamos en la imagen adjunta:
Este vector es el mismo que el que comienza en el punto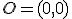 
y termina en el 
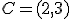ya que 
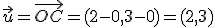. Así, al igual que la Fuerza que hemos aplicado anteriormente, que es una magnitud vectorial, es decir, que va a venir expresada por un vector, los vectores van a venir dado por tres características.
 |
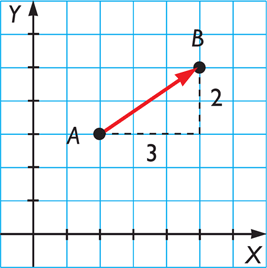La primera es la dirección, que es la recta sobre la que se encuentra, la otra es el sentido que viene determinado por el sentido al que apunta la flecha del vector sobre la recta, en nuestro ejemplo anterior podemos observar que no es lo mismo el vector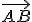 
que el vector 
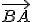. Por último, la tercera característica de un vector es su longitud, su módulo (como es la longitud que mide es positiva).
En la imagen de la derecha hemos representado el vector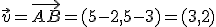 
. En este caso, para calcular el módulo del vector que es la longitud del vector 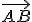, vamos a aplicar el teorema de Pitágoras. El módulo del vector se denota de la siguiente forma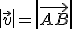 
De esta forma tenemos que 
Observamos entonces que si tenemos un vector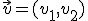 
su módulo es: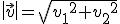 
La primera de estas operaciones es la suma de vectores. Si tenemos dos vectores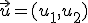 
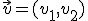y la suma de los dos se obtiene algebraicamente:
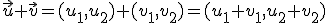. De forma gráfica la puedes realizar en la escena de abajo. Suma allí los vectores 
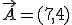y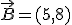 
.
| En la escena de abajo puedes sumar dos vectores en el plano. Para ello mueve los puntos azules que marcan el origen y el extremo de los vectores (en rojo) que quieres sumar para definirlos. Para cada par de vectores te aparecerá el vector suma (en trazo verde discontinuo) correspondiente. |
AV - Actividad de Espacios en Blanco
, 
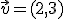y 
del espacio de dos dimensiones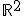 
, calcules los vectores
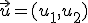y un número 
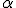se tiene que 
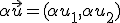que observamos que es otro vector.Por ejemplo, si tenemos un vector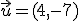 
, el vector 
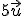es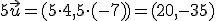 
.
| En la escena de abajo puedes ver el vector v=(2,2) el cual al multiplicarlo por el escalar c=3 se obtiene un nuevo vector marcado en trazo azul discontinuo de coordenadas (6,6). Puedes modificar el vector v de partida moviendo su extremo con el ratón, así como el valor del escalar c moviendo la barra deslizante de la parte inferior derecha, obteniendo otros resultados diferentes. |
Ejemplo o ejercicio resuelto
¿Sabías que a la hora de desplazar un objeto arrastrándolo aparece una fuerza que se opone al movimiento? Esta fuerza se llama fuerza de rozamiento. Aprende algo más sobre ella aquí:
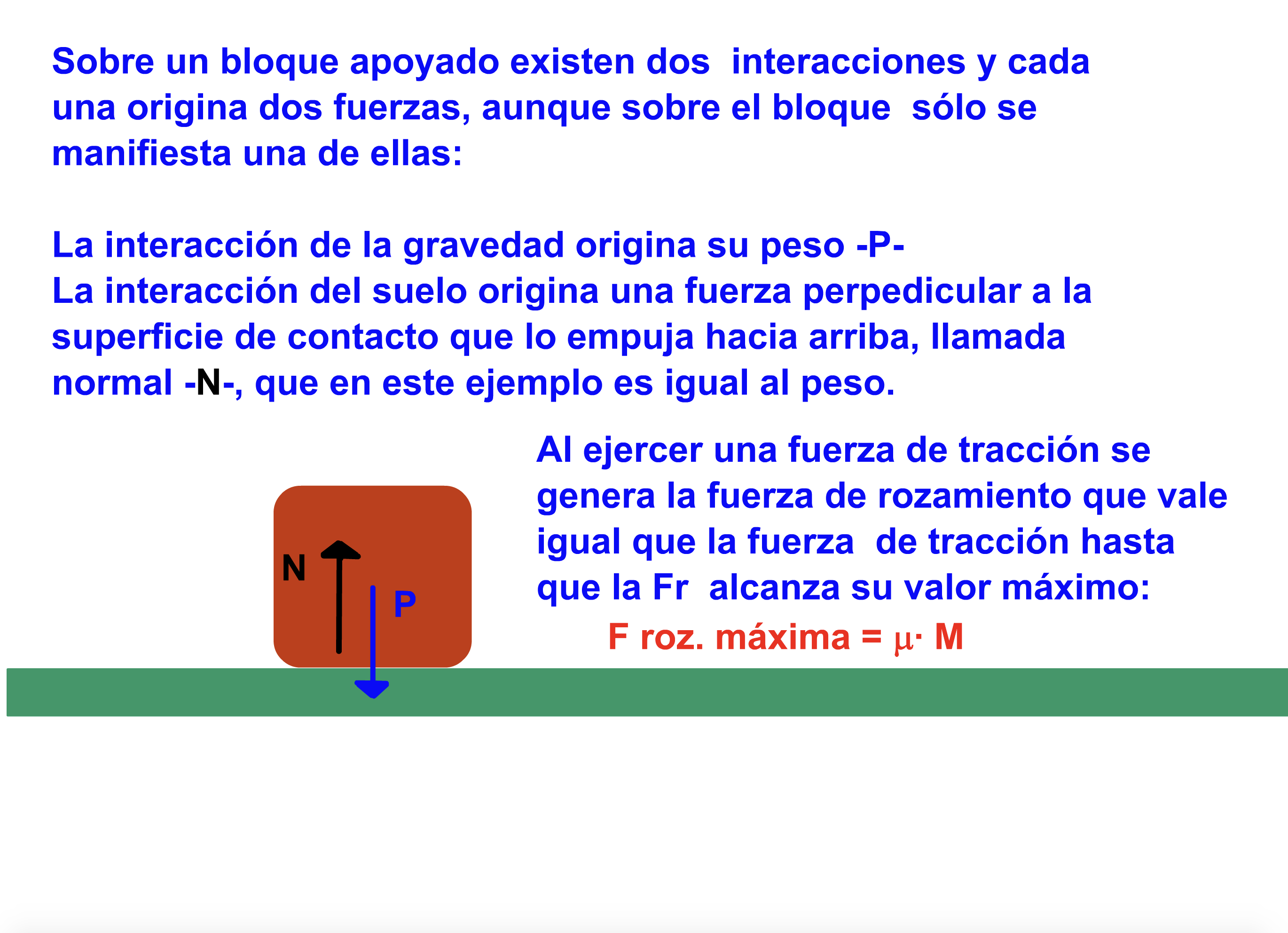
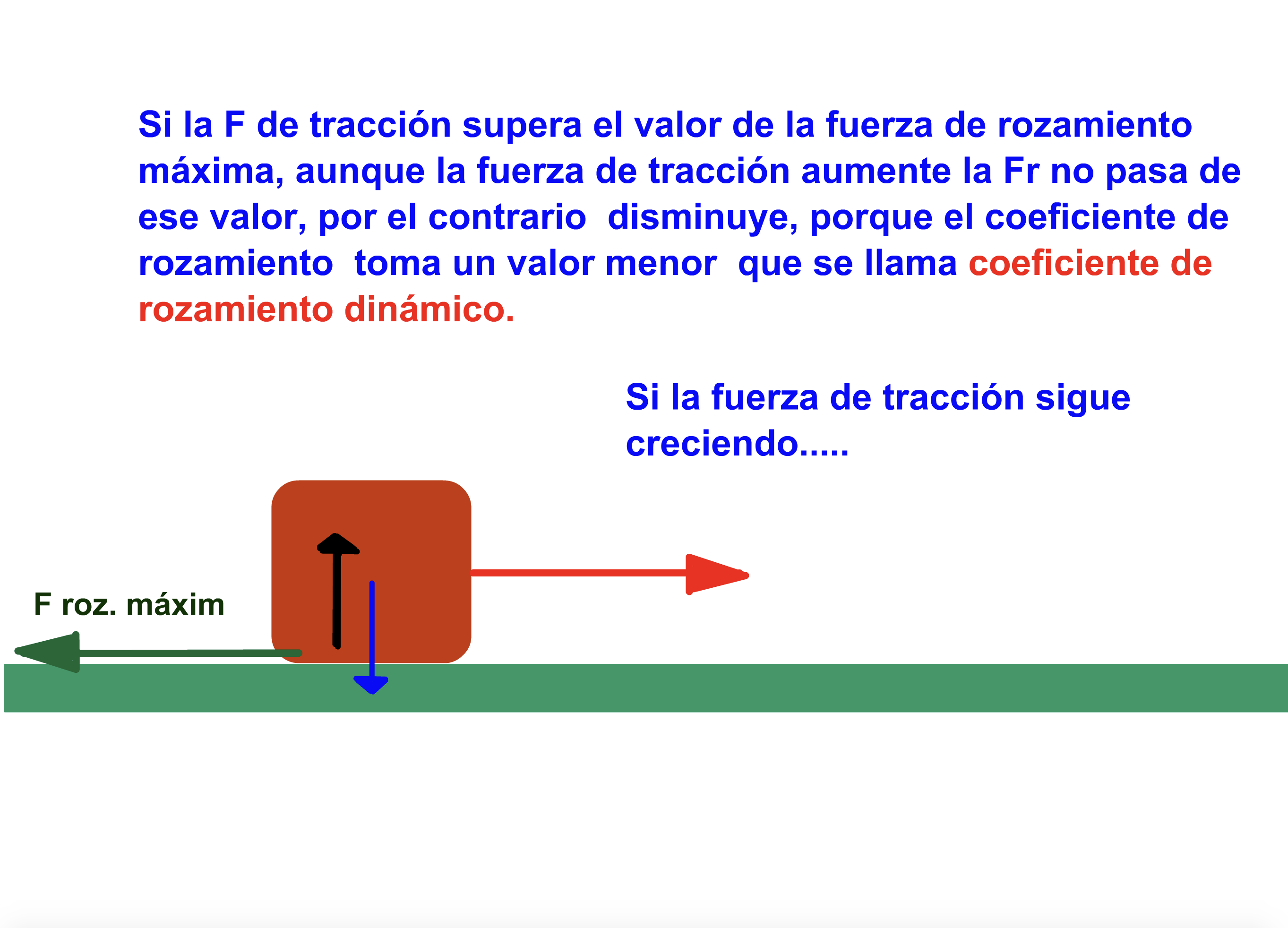
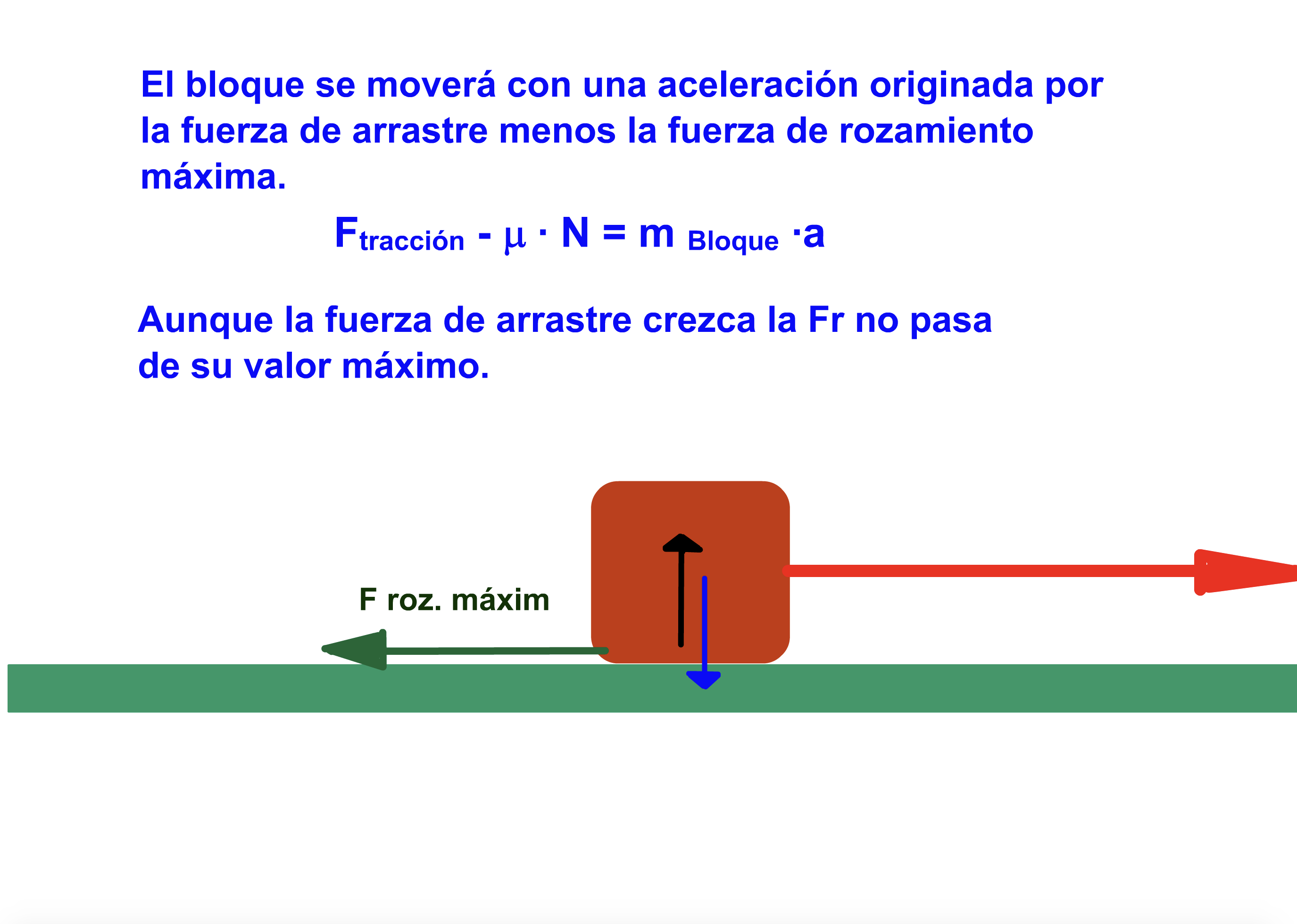
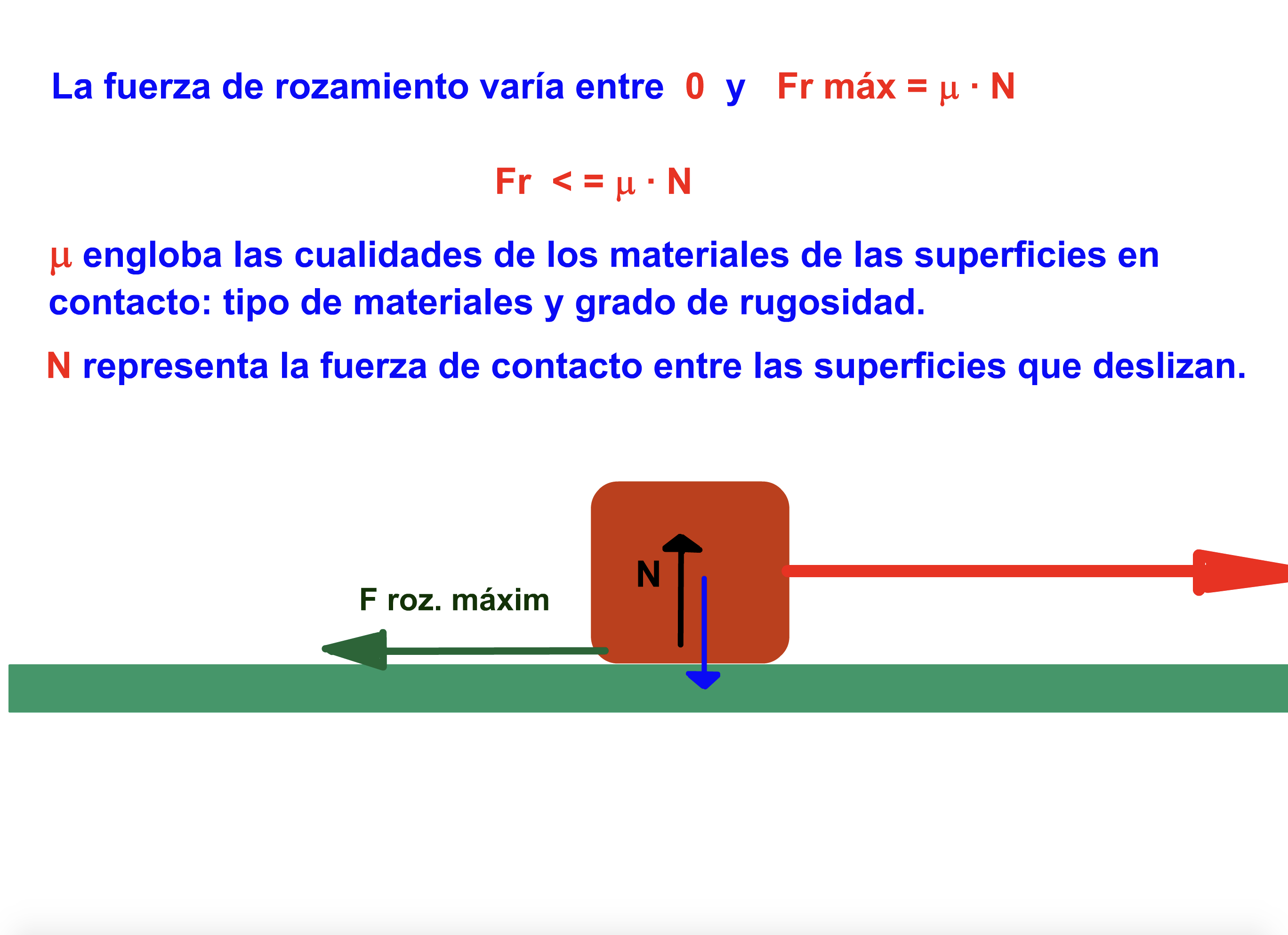
Imagina que tenemos un objeto cuadrado sobre el que están empujando dos hombres por dos caras consecutivas. Si el primero de los hombres está aplicando una fuerza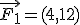 
y el segundo está aplicando una fuerza 
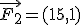y estas fuerzas son las justas para que el objeto no se mueva, calcula la fuerza de rozamiento del objeto con la superficie sobre la que está apoyado.
Para saber más
con las actividades a las que puedes acceder desde los siguientes enlaces. En ellas encontrarás pantallas interactivas que te ayudarán.
1.- VECTORES EN EL PLANOTrabajo con vectores dados gráficamente |
2.- PRACTICANDO CON VECTORESPractica con vectores utilizando coordenadas y componentes en cada una de las actividades |
Curiosidad
René Descartes, nacido el 31 de Marzo de 1596 en La Haye, Touraine, Francia y fallecido el 11 de Febrero de 1650 en Estocolmo, Suecia, usó las coordenadas para representar los puntos y a partir de entonces tenemos las representaciones gráficas y los ejes cartesianos. En realidad cabe destacar que el nombre de ejes cartesianos no se debe a Descartes, sino a un matemático posterior llamado: Maurice René Fréchet (Maligny, 1878-París, 1973) quién las llamó así en honor a Descartes. Conoce más de René Descartes en el siguiente vídeo.