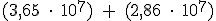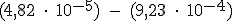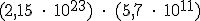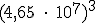5.3. Repaso sobre notación científica
 |
| Imagen de Indolences en Wikimedia Commons bajo CC |
Estos números resulta difícil nombrarlos y escribirlos y por eso nos ayudamos de las potencias para expresarlos de forma más simplificada. La notación científica es una forma particular de escribir estos números utilizando las potencias.
Así la forma de expresar la distancia de la Tierra al Sol como 1,5 · 108 Km, o la masa de un electrón como 9,1 · 10-31 Kg se llama notación científica.
Actividad
Una cantidad se expresa en notación científica como un número por una potencia de 10 (de exponente positivo o negativo). Dicho número tiene que cumplir unas condiciones:
- Si es entero tiene que tener una sola cifra, por ejemplo: 5 · 107.
- Si es decimal, la parte entera tiene que tener una sola cifra del 1 al 9, es decir, la parte entera no puede ser cero.
Veamos algunos ejemplos que nos pueden ayudar a la hora de expresar un número en notación científica, en los que se observa que al multiplicar un número por una potencia de 10 de exponente positivo, lo que hacemos es multiplicar por la unidad seguida de tantos ceros como indique el exponente, mientras que al multiplicar por una potencia de 10 de exponente negativo, lo que hacemos es dividir por la unidad seguida de tantos ceros como indique el exponente :
| a · 10n |
a · 10-n |
| 50 = 5 ·10 |
0,5 = 5 : 10 = 5 · 10-1 |
| 500 = 5 · 100 = 5 · 102 |
0,05 = 5 : 100 = 5 · 10-2 |
| 5000 = 5 · 1000 = 5 · 103 |
0,005 = 5 : 1000 = 5 · 10-3 |
| 50000 = 5 · 10000 = 5 · 104 |
0,0005 = 5 : 10000 = 5 ·10-4 |
| 500000 = 5 · 100000 = 5 · 105 |
0,00005 = 5 : 100000 = 5 · 10-5 |
| 5000000 = 5 · 1000000 = 5 · 106 |
0,000005 = 5 : 1000000 = 5 · 10-6 |
Caso de estudio
 |
| Imagen de CeDeC en Flickr . CC |
Expresa los siguientes números en notación científica:
a) 3.000.000
b) 34.000.000.000
c) 235 · 106
d) 0,000003
e) 0, 000000632
f) 234,7 · 10-10
Pregunta de Elección Múltiple
La tecla EXP
 |
| Imagen de elaboración propia |
Esta tecla la tenemos en la parte de abajo de la calculadora, junto a la tecla del punto decimal, y nos sirve para escribir la potencia de 10 del número en notación científica. Veamos un ejemplo para explicarnos mejor.
Supongamos que queremos escribir en la calculadora la expresión: 
, pues bien, en ese caso debemos teclear en la calculadora lo siguiente:
y la calculadora nos mostrará 
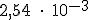; debemos hacerlo como sigue: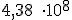
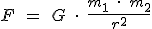y la calculadora nos mostrará 
esto quiere decir 
, sabiendo los siguientes datos:
; 
;
; 
![]().JPG){kind=small}
, que debemos interpretar, una vez redondeado a dos decimales, como: 
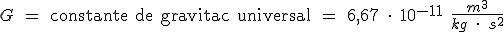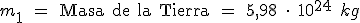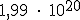
En cuanto a las raíces, veamos otro ejemplo de astronomía, la Tercera ley de Kepler, que nos dice que "el cuadrado de periodo de revolución de un planeta alrededor del Sol, es proporcional al cubo de la distancia del planeta al Sol". Esto lo podemos formular de la siguiente manera:
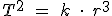; donde k es la constante de proporcionalidad que es igual para todos los planetas. En realidad,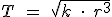 
Podemos ahora calcular el periodo de revolución de nuestra querida Tierra alrededor del Sol. Para ello solo necesitamos saber el valor de k y la distancia media de la Tierra al Sol:
; 
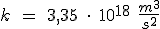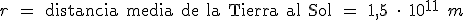
En la calculadora tecleamos:
Y la calculadora nos contestará: 
; que tenemos que leer como: 
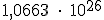evidentemente en segundos, que al pasarlo a días nos sale aproximadamente 365 días, al pasarlo a meses la solución es 12, y en años la solución es 1 año.
Caso de estudio
