Para terminar este tema sobre la descripción del movimiento, os hago esta pregunta:

¿cómo podemos saber si un objeto está realmente quieto o, si por el contrario, se está moviendo?

Ya sabes que dependerá del sistema de referencia que tomes. Recuerda: una mochila a los pies de un estudiante en un autobús escolar estará quieta a los ojos de su dueño, sin embargo se mueve respecto de la parada del bus (al avanzar el autobús, la mochila se aleja, junto con el propio vehículo, obviamente). 

Queda claro que el movimiento que sigue un objeto dependerá del sistema de referencia considerado: se concluye por tanto que el movimiento es relativo.

Imagina que deseamos estudiar algún evento (una pelota que cae, una persona caminando,...) desde dos puntos de vista:

• Desde el interior del vagón de un tren que viaja con cierta velocidad v_t. Este es nuestro sistema de referencia S'. 
• Desde el andén, que está reposo. Este será nuestro sistema de referencia S.

Los sistemas de referencia S y S´, inerciales, se representan en la figura siguiente:

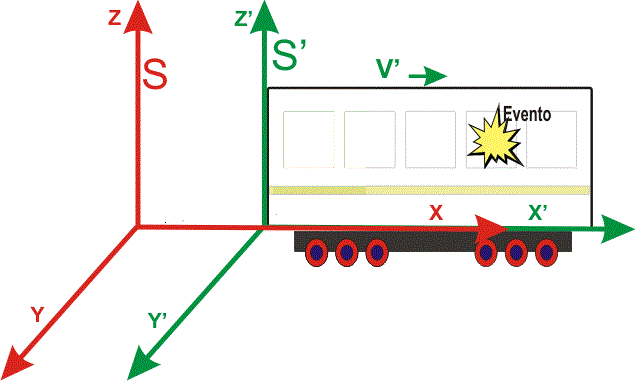
Imagen en Wikimedia Commons de Juancarcole. CC

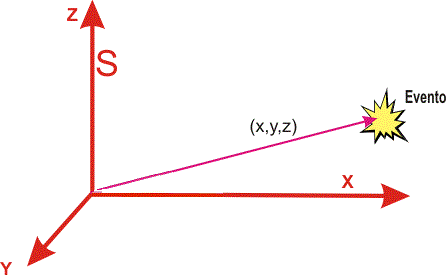
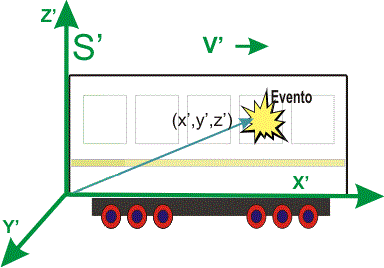
Fíjate ahora en los dibujos siguientes: La posición del evento que según el sistema de referencia S (el andén, en reposo) se describe por las coordenadas (x,y,z). Sin embargo, la posición del mismo evento medido según el sistema de referencia S´(el propio tren, en movimiento) se describe por (x',y',z') El tren (sistema S´) se mueve hacia la derecha con una velocidad constante v_t. Si elegimos como instante inicial el momento en que el tren pasa justo por un punto concreto del andén (sistema S), podremos escribir x₀=x'₀=0 que son las posiciones iniciales. Además, conforme el tren se va desplazando, su posición respecto del andén puede obtenerse x=v_t·t. 

Imagen en Wikimedia Commons de Juancarcole. CC	Imagen en Wikimedia Commons de Juancarcole. CC

Como el tren se mueve en el eje horizontal, podemos afirmar que las coordenadas y y z son las mismas en ambos sistemas de referencia. Además puesto que el tren se mueve a velocidad v_t, la coordenada x irá aumentando conforme el tren se aleja. En resumen, obtenemos unas expresiones como estas:

Si determinamos las velocidades y las aceleraciones se cumple:

• la velocidad según S´ (v') es la velocidad medida desde S (v) menos la velocidad del tren (v_t):

• y, lo más importante, las aceleraciones coinciden:

  {a}'=a

La implicación de todo esto es que, como desde los dos sistemas de referencia medimos la misma aceleración, las fuerzas que explican el movimiento (en la unidad siguiente verás que F=m·a) son las misma en ambos sistemas.

Traducido al lenguaje común esto significa que no hay ninguna diferencia entre un sistema en reposo o un sistema que se mueva con velocidad constante respeto de él. Lo cierto es que de esto tenemos muchas experiencias: por ejemplo si estás en un ascensor cerrado al exterior que sube o baja con velocidad constante no podrías distinguir si está en reposo o movimiento, sólo detectas cambios cuando el ascensor frena o acelera (donde la velocidad deja de ser constante).

En el ejemplo del movimiento de caída de un objeto que hemos visto en el apartado 2 (barco), los dos observadores pueden explicar el movimiento simplemente por acción de la gravedad. La diferencia entre ellos está en que, respecto del observador en reposo, el objeto lleva una velocidad horizontal inicial cuando cae, lo que le obliga a describir una trayectoria parabólica. Pero las fuerzas serán las mismas en ambos sistemas.

 Gracias por tanto al principio de relatividad de Galileo, podremos estudiar un sistema tomando el sistema de referencia que más convenga, a nuestra elección.