Como ya hemos visto en la definición de la velocidad esta magnitud tiene carácter vectorial y, por tanto, se representa por medio de un vector. Dicho vector tiene como módulo el valor de la rapidez, es tangente a la trayectoria en cada momento del movimiento y el sentido será el del movimiento.
La mayoría de los movimientos a los que estamos habituados se producen en el plano. Podemos utilizar un sistema de referencia cartesiano para describirlos.
En la siguiente figura podemos ver cómo se descompone el vector velocidad en función de las componentes cartesianas x e y.
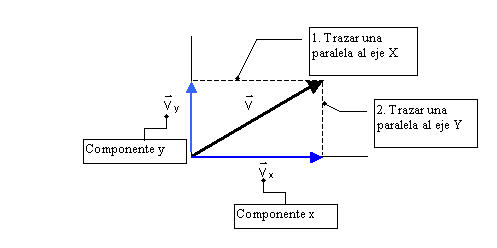
Dibujo de autor desconocido
La expresión de la velocidad queda de la siguiente forma:
v = \frac{\bigtriangleup e}{\bigtriangleup t} = \frac {e_f - e_0}{t_f - t_0}
Expresión de la velocidad que en función de los vectores unitarios i y j viene dada por:
\vec{v} = \vec{v_x}+\vec{v_y}
Determinación de la rapidez
Sabemos que la rapidez se corresponde con el módulo del vector velocidad. Aplicando el teorema de Pitágoras, como ya se ha visto antes con el vector de posición, podremos calcular el valor de rapidez.
\| \vec{v} \| = \sqrt{v_x^2+v_y^2}
Significado de la velocidad negativa
¿Qué quiere decir que un móvil lleva velocidad negativa? Vamos a analizar el caso más sencillo, comparando el caso de dos objetos que se mueven sobre la misma línea recta, que tomaremos como sistema de referencia, llevando velocidades respectivas y constantes de 5 m/s el móvil A y de -5 m/s el móvil B.
Vectorialmente, ambas velocidades se expresan como:
\vec v_1 = + 5 \vec i m/s \\ \vec v_2 = -5 \vec i m/s
En ambos casos, el módulo del vector es 5, por lo que la rapidez del movimiento también es 5. Es decir, los dos móviles recorren 5 metros en cada segundo.Entonces ¿dónde está la diferencia?:
La diferencia radica en que el móvil A se mueve en el sentido positivo del desplazamiento mientras que el móvil B lo hace en el sentido negativco del desplazamiento.
