1. Unificación de campos eléctrico y magnético
|
|
El apoyo a las ideas de Huygens se incrementa notablemente durante los comienzos del siglo XIX, pero el modelo necesita tener un trasfondo matemático y establecer el patrón que permita clasificar la luz dentro de los tipos de ondas.
Pues bien, unos de los mayores genios de la Física por sus dotes interpretativas y capacidad de síntesis es, sin lugar a dudas, James C. Maxwell.
A finales del siglo XIX, en pleno estudio de la electricidad y el magnetismo, intuyó la existencia de una relación entre ambos campos, magnéticos y eléctricos.
Recuerda que un campo magnético variable a lo largo del tiempo es capaz de inducir un campo eléctrico, luego, Maxwell, teniendo en cuenta lo anterior propuso que, así mismo, un campo eléctrico variable debía inducir un campo magnético.
Aquí, para este monstruo, no quedó la cosa, logró hacer por primera vez una fusión de teorías, es decir una teoría unificada o unificadora a tu gusto. Dicho de otra forma, juntó todas las leyes básicas de la electricidad y el magnetismo en cuatro ecuaciones, que, hoy, se conocen por el nombre de ecuaciones de Maxwell y que fueron publicadas en el año 1873 en el un tratado que tenía por título Treatise on Electricity and Magnetism, donde estableció la teoría electromagnética. El libro fue considerado como el texto definitivo.
Dentro de las cuestiones importantes que incluían sus ideas, era que que la oscilación de una carga eléctrica crea un campo eléctrico variable y éste a su vez un campo magnético que varia de forma conjunta con el anterior.
Un pasito para la luz.
Objetivos
Las ecuaciones de Maxwell:
Son la traducción al lenguaje matemático las leyes propuestas por Coulomb, Biot y Savart, Ampere y Faraday-Henry
Ley de Gauss para el campo eléctrico.

La interpretación de la ecuación viene a exponer que el flujo del vector intensidad de campo eléctrico a través de una superficie está en relación con la carga que encierra la misma. Con ello, se consigue describir cómo las líneas de campo se dirigen hacia las cargas negativas o salen de las positivas. Está claro que debe tener un sustento experimental el mismo corresponde a la ley de Coulomb.
Ley de Gauss para el campo magnético.
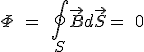
Al igual que la anterior viene a indicar que el flujo del vector inducción magnética o campo magnético a través de una superficie cerrada, pero en este caso es cero, es decir, el número de líneas de campo que entran y que salen coinciden. Es evidente que está en consonancia con lo experimental que indica que las líneas del campo magnético no divergen ni convergen en ningún punto del espacio, es decir, no existen polos magnéticos aislados. Aunque recientemente ha habido un descubrimiento que revolucionara la Física actual, la existencia de monopolos magnéticos.
Ley de Faraday-Henry.
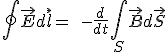
La expresión vienen a indicar el modo de generación de un campo eléctrico gracias al cambio temporal de un campo magnético. La ecuación tiene como base el fenómeno de inducción magnética.
Ley de Ampère-Maxwell o Ley de Ampère generalizada.
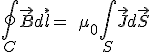
La ley de Ampère cuantificaba el campo magnético debido a corrientes eléctricas. Maxwell amplió la idea para que también incluyera la producción del campo magnético debido a campos eléctricos variables.
Todas estas ecuaciones buscan ser una forma de secundar la teoría de campo, a la cual tenía una firme fe. Llegó a establecer unas analogías mecánicas para poner de manifiesto el comportamiento de los campos en el espacio y como eran transportadas las influencias magnéticas y eléctricas por esa zona gracias a dientes invisibles de circulación.
¿Quizás los fotones tengan algo que ver?
