2.1. Ejemplo 1

Retroalimentación

1^er paso: Encontrar la función.

Lo que queremos que sea mínimo es el área total de la lata, por tanto, vamos a empezar construyendo esa área.

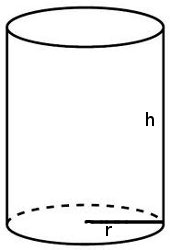
El área total queda determinado por la suma del área lateral y el de las dos tapas. El área lateral es un rectángulo cuya altura es la altura del cilindro (h) y cuya base es la longitud de la circunferencia que da el borde, o sea, 2πr. Luego el área lateral del cilindro es: A_l = 2·π·r·h

Por otro lado, la base y la tapadera son sendos círculos y como recordarás, el área de un círculo es π·r².

Por tanto, el área total de la lata de refrescos es: A_T = 2·π·r·h + 2·π·r²

Todavía no nos vale porque tenemos dos variables, el radio de la base, r, y la altura del cilindro, h, así que, hemos de poner una en función de la otra. Para ello, usamos el dato de que la lata ha de ser de un tercio de litro. Puesto que queremos relacionar unidades de volumen con longitudes o áreas, el volumen lo tenemos que expresar en unidades cúbicas, o sea, m³, cm³, etc., así que como dato, usaremos que el volumen de la lata es 333 cm³

El volumen de un cilindro se calcula a partir de la fórmula V = π·r²·h, (área de la base por la altura). Por tanto, ha de ser,

Puesto que es más fácil despejar la altura, (si despejas r, habría que poner raíz cuadrada), nos queda que: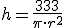

Sustituyendo en el área total, nos queda: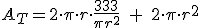

Y simplificando: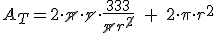

Luego la función a minimizar es: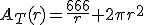

2º Paso: Derivar e igualar a cero.

Tenemos que tener en cuenta que la función es a su vez suma de dos partes y que la variable es r. Derivando obtenemos:

Igualamos a cero la derivada para buscar los puntos candidatos a extremo relativo:

Resolviendo la ecuación obtenemos como solución aproximada: r≈3,76 cm.

Imagen de JavierPsilocybin bajo licencia Creative Commons

3^er Paso: Comprobar la solución.

Vamos a comprobar que efectivamente ese valor de r es un mínimo, para ello, calculamos la segunda derivada, sustituimos ese valor y debe de salirnos un resultado positivo.

Derivando el resultado obtenido en la primera derivada, obtenemos que la segunda derivada es:

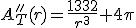
Sustituyendo el valor de r obtenido anteriormente: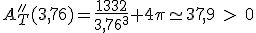

Como puedes ver, una cantidad positiva, por tanto, ese valor es un mínimo relativo.

Además, sustituyendo en la función área, tenemos que el área asociado a ese valor de r es: 265,91 cm²

Ahora bien, ¿puede haber otro valor mínimo? La respuesta es no, pues el radio tiene que ser una cantidad positiva (>0) y puede ser todo lo grande que queramos, sería cuestión de estrechar la lata. El dominio real de nuestra función área total es el intervalo (0,+∞), luego no puede haber otro mínimo aparte del relativo al no ser un intervalo cerrado.

Así pues, r= 3,76 cm es el radio de la lata de mínimo coste, y sustituyendo donde habíamos despejado la altura, obtenemos que la altura es:

Luego la mejor lata de un tercio de litro que podemos construir es la que mide aproximadamente 3,76 cm de radio y 7,5 cm de altura.

Y ahora vete al frigo y mide una lata, a ver si varía mucho. Si lo crees necesario puedes llamar al fabricante y decirle que aún puede ganar más.