2.2. Funciones polinómicas y racionales
Apenas hemos iniciado el tema y ya has puesto en práctica una gran cantidad de conocimientos que poseías sobre las funciones y que has aplicado al ver su gráfica.
Además, hemos recogido en el cuadro-resumen del apartado anterior, un procedimiento que debes tener presente a la hora de abordar el análisis y la representación de la gráfica de cualquier función.
Este punto lo dedicaremos única y exclusivamente a abordar la representación gráfica y el estudio de las funciones polinómicas y racionales.
 |
|
Imagen de Stinging Eyes en Flickr. Licencia CC BY-SA 2.0 |
Importante
Una función polinómica es aquella cuya expresión es un polinomio. Su expresión general es:
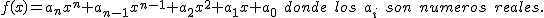
Ya has trabajado con funciones polinómicas a lo largo del curso:
+ Las funciones polinómicas de grado 1 son las funciones lineales (sus gráficas son líneas rectas)
+ Las funciones polinómicas de grado 2 son las funciones cuadráticas (sus gráficas son parábolas)
Todas las funciones polinómicas presentan una serie de características, atributos, comunes. Es normal, la genética, también juega su papel en entre las funciones miembros de una misma familia. Son las siguientes:
| Características comunes a todas las funciones polinómicas |
|
|
|
|
|
|
A continuación vamos a efectuar la representación e interpretación de la gráfica de una función polinómica con ayuda de Geogebra para poner en práctica las características de las funciones polinómicas.
|
Vídeo de Luis Miguel Iglesias Albarrán alojado en Youtube.
|
Comprueba lo aprendido
Importante
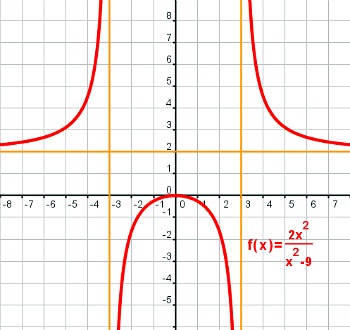
Una función es racional si es el cociente de dos polinomios. Su expresión general es:
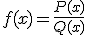
Como bien sabes, los componentes de una misma familia comparten ciertos parecidos razonables sobre todo en sus rasgos físicos, los más perceptibles a primera vista.
Pues, de igual modo que ocurre en seres vivos y que hemos visto anteriormente que sucedía con las funciones polinómicas, en el caso de las funciones racionales, su imagen, es decir, sus gráficas, también comparten ciertas características comunes. Se enumeran a continuación:
| Características comunes a todas las funciones racionales |
Dom(f) =
 \ { \ { 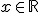 , tales que Q(x)=0} , tales que Q(x)=0} |
|
|
|
Comprueba lo aprendido
Haz una representación de la siguiente función usando Geogebra:
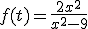
Finalmente, rellena las huecos en blanco.
Curiosidad
Antes de continuar con el tema, ¿por qué no nos pegamos frente al espejo unos buenos movimientos de baile practicando con la gráfica de algunas de las funciones más conocidas? ¿Te animas?