2.1. Intervalos, semirrectas y distancias
Es posible que, estudiando o leyendo un libro, te hayas hecho alguna vez un plan de trabajo y hayas formulado comentarios como:
"Hoy me leeré de la 20 a la 40"
Es decir, tienes el proyecto de leer todas las páginas comprendidas entre la 20 y la 40. En esta ocasión estás usando intervalos para dar una información.
Importante
Si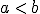 
se llama intervalo de extremos 
y 
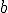al conjunto de números que están entre y 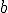en la relación de orden. Según contengan o no los extremos los intervalos se llaman cerrados o abiertos, respectivamente; o semicerrados (o semiabiertos) si contienen solamente uno de los extremos.
Es decir, los intervalos son algo así como "trozos" de la recta real.
En la siguiente imagen puedes ver cómo representamos los distintos tramos:
 |
| Imagen de elaboración propia |
Si observas la imagen anterior podrás ver que existen distintas formas de expresar un intervalo:
- Gráficamente: utilizando la recta real e indicando los extremos del intervalo.
- A través de conjunto y desigualdades.
- Usando la notación de intervalo. En este caso, observa que en las semirrectas infinito nunca está contenido.
En el siguiente vídeo puedes ver los diferentes tipos de intervalos.
Vídeo de Tuto mate alojado en Youtube.
Importante
Recuerda que los intervalos se simbolizan mediante corchetes [ ] o paréntesis ( ) dependiendo de si queremos o no incluir los extremos.
Ejercicio Resuelto
Escribe como intervalo los siguientes conjuntos de números reales:
a) Los números que están entre 3 y 10:
b) Los números mayores que 0 y menores o iguales que 8'5:
c) Los números menores que 2/3:
Comprueba lo aprendido
 |
| Imagen de elaboración propia |
Al igual que operábamos con números, con los intervalos podemos hacer algunas operaciones:
- Unión (U): al unir dos intervalos, consideramos los números que están en uno u otro intervalo:
[1,4] U (3,5) = [1,5)
- Intersección (∩): la intersección de dos intervalos consiste en quedarse con los números que están en los dos a la vez:
[1,4] ∩ (3,5) = (3,4]
En los siguientes vídeos puedes ver cómo realizar la unión y la intersección de intervalos:
Comprueba lo aprendido
Retroalimentación
Verdadero
Ya que (1, 3] ∪ (2, 6) = (1, 6)
El ser humano, desde el comienzo de la historia, ha tenido la necesidad de medir para mejorar sus condiciones de vida: medir el tiempo, las distancias, el peso del producto que tenía que vender...
En todos estos casos, lo que realmente estaba haciendo era medir distancias entre los números de la recta real.
Reflexiona
Mueve los puntos A y B y observa cómo varía la distancia.
¿Cómo medimos esa distancia? Es algo muy intuitivo pues sólo tienes que restar los números para ver la diferencia entre ambos.
Veamos las distancias en el siguiente ejemplo:
a) Entre B y C: de 1 a 4 hay 3 unidades que se corresponden con el resultado de la operación 4 - 1 = 3.
b) Entre A y C: de -3 a 4 hay 7 unidades que se corresponden con el resultado de la operación 4 - (-3) = 4 + 3 = 7.