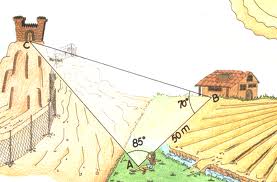
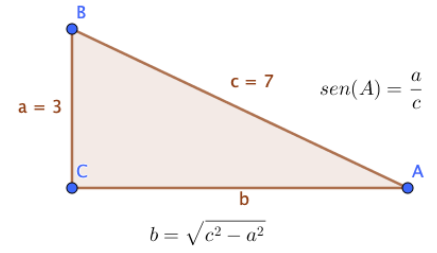
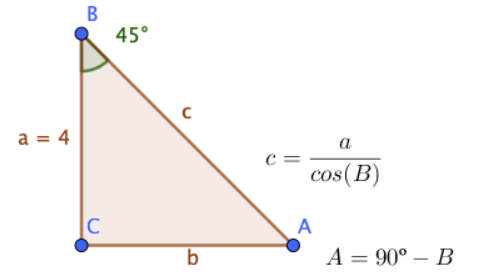
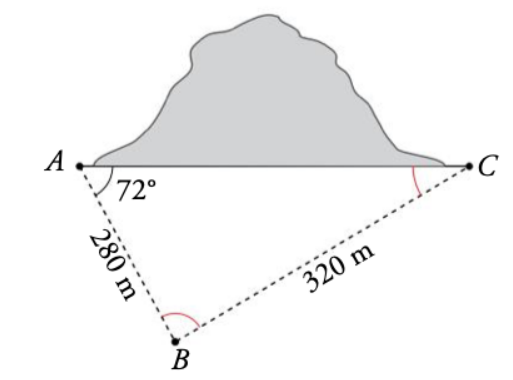
Si por los datos que nos da el ejercicio nos conviniese más coger esta altura \( h\ =\ \overline{CP} \), ahora podríamos aplicar los “poderes” matemáticos que hemos visto, puesto que tenemos a un lado y a otro sendos triángulos rectángulos. Entonces podríamos aplicar:
Altura de un árbol por el método de doble observación y estrategia de la altura
Fíjate, ¿recuerdas el teodolito o inclinómetro que construimos en la fase 3? Ahora vamos a utilizarlo para hallar la altura de un árbol a través del método de doble observación y a través de la estrategia de la altura.

Figura obtenida de la situación real
Esta es la figura que obtenemos. Efectivamente medir la altura del árbol que está al otro lado del río es imposible, pero utilizando nuestros poderes matemáticos vamos a hacerlo. Si dibujamos la situación que tenemos, sería una cosa así:

Situados en C lanzamos una visual al punto más alto del árbol y obtenemos un ángulo \( \alpha\ =\ 32º\ 42''\). A continuación avanzamos 12 metros en dirección al árbol, para situarnos en el punto D y volvemos a hacer lo mismo y nuestro teodolito nos da un ángulo \( \beta\ =\ 52º\ 26'\ 53'' \).
Planteamiento y a qué llamamos x
Vamos a calcular la altura del árbol, teniendo en cuenta que la altura en la que hago la observación con el teodolito es de 1,35 m.

Llamamos \(x=\overline{BA}\). La altura del árbol será por tanto $x+1.35$ porque hay que tener en cuenta la altura del teodolito.
En el triángulo $\overset{\LARGE\Delta}{ABD}$
$$tg\,\beta=\frac{\overline{BA}} {\overline{AD}} \,\,\,\rightarrow\,\,\, tg\,(\,52^{\circ}\,26^{'}\,53^{"})=\frac{x} {d} $$
Obtención del sistema de ecuaciones

Por otra parte, en el triángulo $\overset{\LARGE\Delta}{ABC}$
$$tg\,\alpha=\frac{\overline{BA}} {\overline{AC}} \,\,\,\rightarrow\,\,\, tg\,(\,32^{\circ}\,42^{"})=\frac{x} {d+12} $$
Obtenemos el siguiente sistema de ecuaciones:
$$ \left\{ \begin{array}{ l } tg\,(\,52^{\circ}\,26^{'}\,53^{"})=\Large\frac{x} {d} \\ tg\,(32^{\circ}\,42^{"})=\Large\frac{x} {d+12} \end{array} \right. \rightarrow \left\{ \begin{array}{ l } 1.3=\Large\frac{x} {d} \\ 0.63=\Large\frac{x} {d+12} \end{array} \right. $$
Resolución del sistema de ecuaciones
¿Recuerdas los sistemas de ecuaciones de otros años? Podíamos resolverlos por 3 métodos, igualación, sustitución o reducción. Vamos a hacerlo por este último despejando $x$ en ambas ecuaciones e igualando:
$$ \left\{ \begin{array}{ l } 1.3=\Large\frac{x} {d} \\ 0.63=\Large\frac{x} {d+12} \end{array} \right. $$
$$1.3\,·\,d\,=\,0.63\,(d+12)\rightarrow0.67\,·d=7.56\rightarrow d=11.28\,m$$
Y despejando la x de una de las ecuaciones, por ejemplo la primera:
$$1.3=\frac{x} {d}\rightarrow x=1.3\,·11.28=14.66\,m$$
Por tanto la altura del árbol es:
$$x+1.35=14.66+1.35=\bbox [5px , border:2px solid red]{16.01\,m}$$
Haz un esquema del proceso seguido y realizamos un debate en clase, en el que entre otras, contestamos a las siguientes preguntas: