4.2. Aplicación del método de Gauss

Lo habitual es que el sistema que nos salga no sea tan fácil de resolver como los que hemos visto en el punto anterior, pero como ya hemos mencionado, la clave consistirá en transformarlo en otro equivalente que sí sea de esa forma triangular.

Para resolver estos sistemas utilizaremos el método de Gauss, que consiste en encontrar otro sistema con la misma solución en el que cada una de las ecuaciones tiene una incógnita menos que la anterior.

Para conseguirlo podemos usar las siguientes transformaciones:

  • Cambiar de orden dos ecuaciones.
  • Multiplicar o dividir los dos miembros de una ecuación por un mismo número.
  • Cambiar una ecuación por la suma de ésta más otra ecuación.

 Si te fijas, estas transformaciones son las mismas que aplicábamos en el tema anterior cuando resolvíamos un sistema por el método de reducción. Había que multiplicar las ecuaciones por números para que cuando las sumara una de las incógnitas se fueran.

Vamos a ver con un ejemplo cómo se resuelve un sistema utilizando este método.

En el siguiente vídeo puedes ver los pasos necesarios para resolver un sistema por el método de Gauss.

Vídeo de Píldoras matemáticas alojado en Youtube

Caso práctico

Bolsa

Imagen de Megan_Rexazin en Pixabay.  Licencia CC

Tres amigos han decidido invertir parte de sus ahorros comprando acciones de tres valores bursátiles: La empresa aseguradora "XAFXA", el Banco "BANKCESTO" y la constructora "SURCO". Queremos averiguar cuánto valen las acciones de esas empresas y disponemos de la siguiente información:

Sebastián ha comprado 100 acciones de XAFXA, 60 del banco y 20 de la constructora y en total ha pagado 1660 €.

Miguel Ángel ha comprado 60 acciones de la aseguradora, 10 del banco y 100 de la constructora SURCO y ha desembolsado 1570 €.

Por último, Adrián, más confiado en los valores de la construcción, ha invertido de la siguiente forma; 30 acciones de XAFXA y 150 de SURCO y ha gastado 1560 €.

Importante

Como has visto en el ejemplo, el método de Gauss consiste en eliminar los elementos que se encuentran por debajo de la diagonal. Para ello se multiplican las filas por números adecuados para que al sumarlas se vaya el elemento deseado, tal como se hace en el método de reducción para eliminar una incógnita.

Practica con el siguiente applet de Geogebra. Si no sabes seguir o tienes cualquier duda, pulsa la tecla "pista" e irán apareciendo los pasos necesarios para resolver el sistema. Para comprobar la solución introduce los valores y pulsa el botón "comprobar solución".

Applet de Javier Cayetano Rodríguez en Geogebra. Licencia CC

Comprueba lo aprendido

Pregunta

Selecciona las respuestas que sean correctas

Queremos resolver el sistema:

Para eliminar "3x" de la segunda ecuación:

Respuestas

Multiplico la 1ª ecuación por 3 , la segunda la dejo igual y sumo.

Multiplico la 1ª ecuación por -3, la segunda la dejo igual y sumo.

Multiplico la 1ª por 3, la segunda por -1 y sumo.

Retroalimentación

Pregunta

Para eliminar el término -2x de la tercera ecuación:

Respuestas

Multiplico la 1ª ecuación por 2, la tercera la dejo igual y sumo.

Multiplico la 2ª ecuación por 2 y la tercera por 3 y sumo

Multiplico la 1ª ecuación por -2, la tercera por -1 y sumo

Retroalimentación

Comprueba lo aprendido

Completa los cuadros en blanco con los números y signos que correspondan.

Ojo: no dejes espacios en blanco entre los signos y los números. Escríbelo todo seguido.

Para resolver el sistema comenzamos haciendo cero el término 3x. Para ello multiplicamos la primera ecuación por (-3) y le sumamos la segunda, quedando entonces

0x y z = .

Para eliminar el -2x, multiplicamos la primera ecuación por 2 y sumamos con la tercera, quedando ésta entonces 0x y z =

Y por tanto el sistema queda:

1ª Ecuación:

2ª Ecuación:

3ª Ecuación:

Habilitar JavaScript

Reflexiona

Encuentra la solución de los siguientes sistemas usando el método de Gauss:

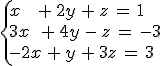        y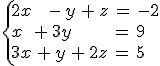    

El método de Gauss lo utilizaremos para resolver distintas situaciones, como podemos apreciar en los siguientes ejemplos:

Problema resuelto: Método de Gauss
Presentación de luanmadi en SlideShare
Problema gauss
Presentación de CarmenMaths en Slideshare

Comprueba lo aprendido

Para que puedas seguir practicando te proporcionamos el siguiente enlace:

Resolución de sistemas de tres ecuaciones con tres incógnitas por el método de Gauss

Curiosidad

A veces suele usarse la notación matricial del sistema para simplificar la escritura como en el siguiente ejemplo. Aquí puedes ver otro sistema resuelto aplicando el método de Gauss.

Vídeo de Miguemáticas alojado en Youtube