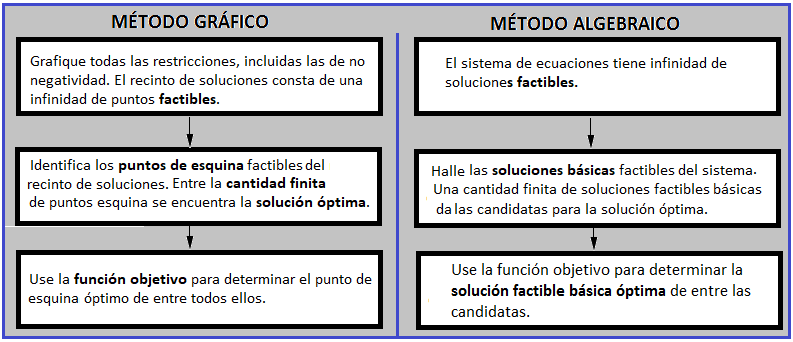
Introducción.- Cualquier problema de minimización equivale a otro de maximización, siempre que las respectivas Funciones Objetivo tengan el signo contrario. Es decir, minimizar $z=f(x_1,x_2,...,x_m)$ equivale a maximizar $z=-f(x_1,x_2,...,x_m)$, donde ambos problemas están sujetos al mismo conjunto de restricciones. Obsérvese que Zmin = −Zmax, aunque el valor óptimo de las variables de ambos problemas coincida. Por ello, nos centraremos en los problemas de maximización.
Sea el problema siguiente en dos variables $(x_1,x_2)$.
Maximiza la función $z=2x_1+3x_2$, sujeta a las siguientes restricciones:
$\left. \begin{array}{l} x_1 \geq 0 \\ x_2 \geq 0 \\x_1+3x_2\leq6 \\ 3x_1+2x_2\leq6 \end{array} \right\} $
En primer lugar expresamos el conjunto de restricciones en modo de sistema de ecuaciones lineales introduciendo las variables de holgura $s_1,s_2\geq 0$.
$\left. \begin{array}{l} z-2x_1-3x_2=0 \\x_1+3x_2+s_1=6 \\3x_1+2x_2+s_2=6 \\ x_1, x_2,s_1,s_2\geq 0 \end{array} \right\} $
Tabulamos toda esta información del modo siguiente:
|
Criterio de Entrada $\rightarrow$
|
$x_1$ |
$x_2$ |
$s_1$ |
$s_2$ |
|
|
|
|
z
|
-2 |
-3 |
0 |
0 |
$z_1=0$ |
Cociente o Razón |
Criterio de Salida $\downarrow$ |
| Variables Básicas |
| $s_1$ |
1 |
3 |
1 |
0 |
6 |
|
|
| $s_2$ |
3 |
2 |
0 |
1 |
6 |
|
|
Primera Toma de decisiones. Variable que entra como Básica y Variable Básica que sale.
Criterio de Entrada $\rightarrow$
$x_2$ |
$x_1$ |
$x_2$ |
$s_1$ |
$s_2$ |
|
|
|
| z |
-2 |
-3 |
0 |
0 |
$z_1=0$ |
Cociente o Razón
$\downarrow$ |
Criterio de Salida $\downarrow$
$s_1$ |
Variables Básicas
|
| $s_1$ |
1 |
3 |
1 |
0 |
6 |
6/3=2 |
$s_1$ |
| $s_2$ |
3 |
2 |
0 |
1 |
6 |
6/2=3 |
|
Sol. Variables Básicas $(s_1,s_2)=(6,6)$
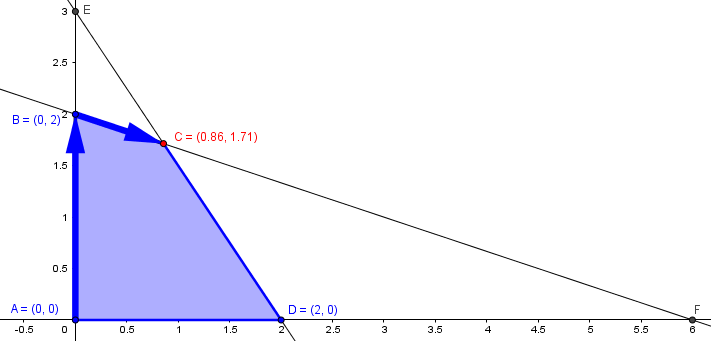
Sol. Factible de Variables No Básicas. Punto esquina.$(x_1,x_2)=A(0,0)$
$z=0$
Criterio de Entrada en la Sol. Básica
$z=2x_1+3x_2$. Un aumento positivo de $x_2$ haría aumentar el valor de z.
Criterio de Salida en la Sol. Básica
La variable $x_2$ no puede salirse del recinto de soluciones. Por tanto, de entre los valores posibles para ella, determinamos la más próxima al anterior vértice y ese punto lo decide el menor de los cocientes positivos
$s_1 \rightarrow \frac{6}{3}=2\rightarrow (x_1,x_2)=(0,2)\rightarrow B=(0,2)\ Punto\ esquina$
$s_2 \rightarrow \frac{6}{2}=3\rightarrow (x_1,x_2)=(0,3)\rightarrow E=(0,3) \ No\ pertenece\ al\ Recinto\ de\ Soluciones$
Por tanto sale como variable básica $s_1$,lo que significa que ahora el valor de $s_1=0$
* Primera Iteración. Normalización de la columna de la nueva variable básica, $x_2$.
Criterio de Entrada $\rightarrow$
$x_1$ |
$x_1$ |
$x_2$ |
$s_1$ |
$s_2$ |
|
|
|
| z |
-1 |
0 |
1 |
0 |
$z_2=6$ |
Cociente o Razón
$\downarrow$
|
Criterio de Salida $\downarrow$
$s_2$
|
| Variables Básicas |
| $x_2$ |
1/3 |
1 |
1/3 |
0 |
2 |
6 |
|
| $s_2$ |
7/3 |
0 |
-2/3 |
1 |
2 |
6/7 |
$s_2$ |
Sol. Variables Básicas $(x_2,s_2)=(2,2)$
Sol. No Básica Factible. Punto esquina.$(x_1,x_2)=B(0,2)$
$z=6$
Criterio de Entrada en la Sol. Básica
$z=x_1-s_1+6$. Un aumento positivo de $x_1$ haría aumentar el valor de z.
Criterio de Salida en la Sol. Básica
La variable $x_1$ no puede salirse del recinto de soluciones. Por tanto, de entre los valores posibles para ella, determinamos la más próxima al anterior vértice y ese punto lo decide el menor de los cocientes positivos
$x_2 \rightarrow \frac{2}{{\large{\frac{1}{3}}}}=6\rightarrow (x_1,x_2)=(6,0)\rightarrow F=(6,0)\ \ No\ pertenece\ al\ Recinto\ de\ Soluciones$
$s_2 \rightarrow \frac{2}{{\large{\frac{7}{3}}}}=\frac{6}{7}\rightarrow (x_1,x_2)=(\frac{6}{7},\frac{12}{7})\rightarrow C=(\frac{6}{7},\frac{12}{7}) Punto\ esquina $
Por tanto sale como variable básica $s_2$,lo que significa que ahora el valor de $s_2=0$
*Segunda Iteración. Normalización de la columna de la nueva variable básica, $x_1$.
| Criterio de Entrada $\rightarrow$ |
$x_1$ |
$x_2$ |
$s_1$ |
$s_2$ |
|
| z |
0 |
0 |
5/7 |
3/7 |
$z_3=48/7$ |
| Variables Básicas |
|
$x_2$
|
0 |
1 |
3/7 |
-1/7 |
12/7 |
| $x_1$ |
1 |
0 |
-2/7 |
3/7 |
6/7 |
Sol. Variables Básicas . $(x_1,x_2)=(\frac{6}{7},\frac{12}{7})$
Sol. No Básica Factible. $(s_1,s_2)=(0,0)$
Punto esquina. $(x_1,x_2)=C(\frac{6}{7},\frac{12}{7})$
$z=\frac{48}{7}$
$z=\frac{48}{7}-\frac{5}{7}s_1-\frac{3}{7}s_2$ .
Ya no hay más posibilidades de aumentar este valor de z. Por tanto hemos encontrado la solución óptima.
Itinerario Gráfico seguido por el Método de Simplex.