3.1. Actividades Método gráfico

Problema.
Maximiza la función $z=f(x,y)=2x+3y$, sujeta a las restricciones:

$\left. \begin{array}{l} 3x+2y \le 6 \\ x+3y \le 6 \\ x \geq 0 \\ y \geq 0 \end{array} \right\} $

Resolución gráfica.-
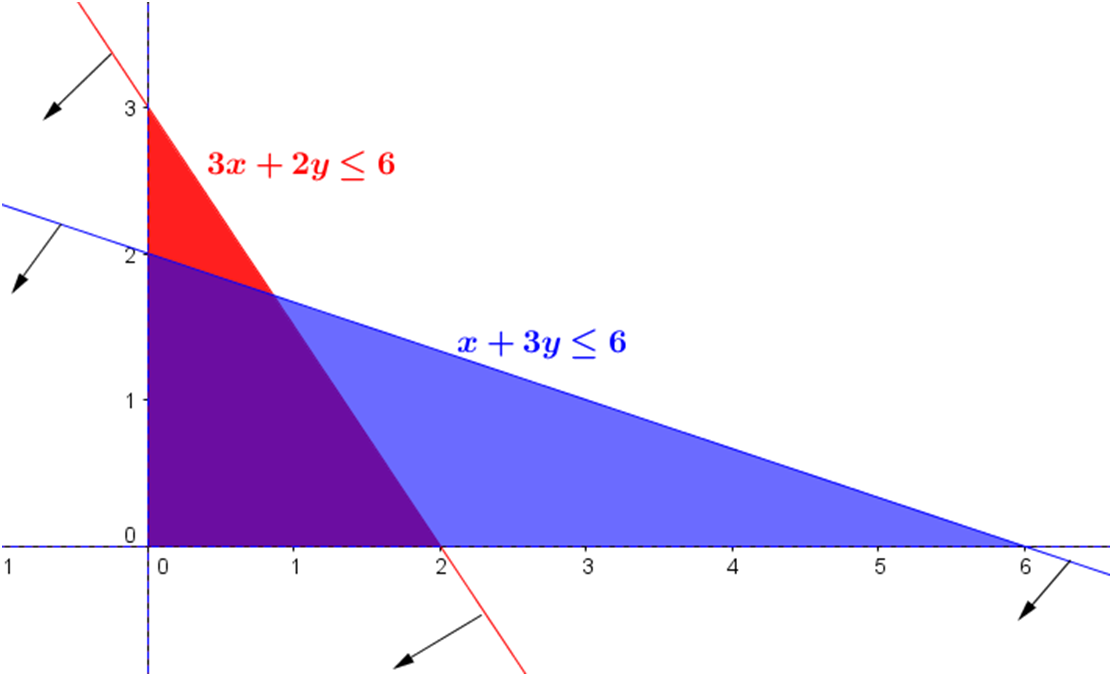
Determinamos las regiones definidas por el conjunto de restricciones. Para ello, representamos las rectas asociadas a cada una de las desigualdades:
(a) $3x+2y=6$. Hallamos dos puntos de la recta como son $(0,3)$ y $(2,0)$.
(b) $x+3y=6$. Procedemos de igual modo, obteniendo los puntos $(0,2)$ y $(6,0)$.
Evaluamos el punto $O:(0,0)$ sobre cada una de las desigualdades para determinar los semiplanos asociados a dichas restricciones.
Para el caso de la primera restricción:
$3x+2y \leq 6$, al sustituir el punto $O:(0,0)$ resulta válida la desigualdad ya que: $3·0+2·0\leq 6 \rightarrow 0\leq6 \rightarrow \text{ cierto}$.
Por tanto, el semiplano al que pertenece el punto O es el que determina esta desigualdad.
Lo mismo ocurre con la desigualdad $x+3y\leq 6$ y el punto $O$ ya que $0+3·0\leq6 \rightarrow 0\leq6\rightarrow \text{ cierto}$.
Como este punto verifica ambas desigualdades, señalamos los semiplanos que debemos elegir. Vemos esto en las siguientes figuras:

Lorem ipsum dolor sit amet...

puedes pulsar sobre la imagen para verla más grande

Imagen de elaboración propia. Conjunto de desiguladades (CC BY-NC-SA)

Lorem ipsum dolor sit amet...

puedes pulsar sobre la imagen para verla más grande

Imagen de elaboración propia. Región factible (CC BY-NC-SA)

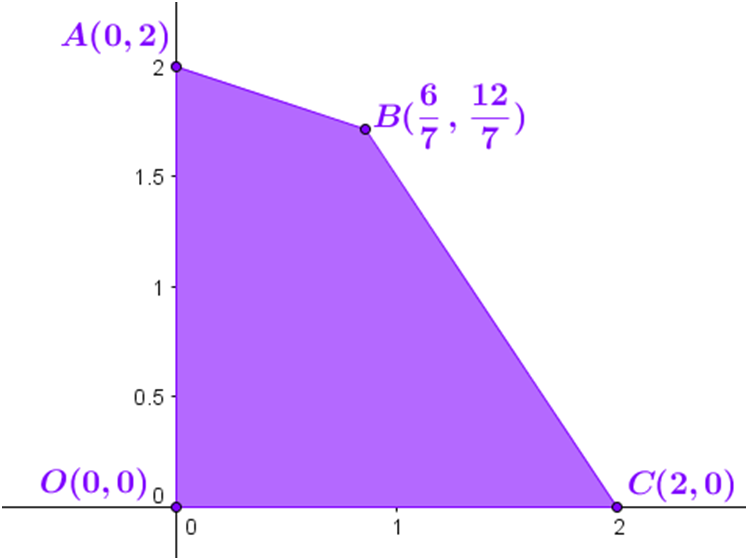
El recinto factible de soluciones resulta ser el cuadrilátero OABC, cuyos vértices tienen las siguientes coordenadas $O(0,0);\ A=(0,2);\ B;\ C=(2,0)$.
Necesitamos hallar las coordenadas del punto B. Este punto pertenece a ambas rectas (a) y (b). Por tanto, si resolvemos el sistema de ecuaciones que nos proporciona ambas rectas, determinaremos sus coordenadas. Lo resolvemos por el método de reducción:

$\begin{matrix} 3x & +2y & =6 \\ -3x & -9y & =-18 \\ \hline \text{  } & -7y & =-12 \end{matrix} $ 

De donde: $-7y=-12 \rightarrow y={\large{\frac{12}{7}}} \rightarrow x+3·{\large{\frac{12}{7}}} =6 \rightarrow x=6-{\large{\frac{36}{7}}} \rightarrow x={\large{\frac{6}{7}}}  $ y por lo tanto el punto B es: $B:\left({\large{\frac{6}{7}}};{\large{\frac{12}{7}}}\right)$ 

Evaluamos ahora la Función Objetivo en los vértices del cuadrilátero ABCD. El mayor de entre estos valores, nos dará la solución de nuestro problema. Como $z=f(x,y)=2x+3y$, sustituimos uno por uno los vértices O, A, B y C en dicha función, este es el procedimiento que hemos hecho hasta ahora, lo repetimos para compararlo con el método gráfico que se usa en apartado siguiente Curvas de Nivel:

$\left. \begin{array}{l} F_O=F(0,0)=2·0+3·0=0 \\ F_A=F(0,2)=2·0+3·2=6 \\ F_B=F \left({\large{\frac{6}{7}}},{\large{\frac{12}{7}}}\right)=2·\left({\large{\frac{6}{7}}}\right)+3·\left({\large{\frac{12}{7}}}\right)={\large{\frac{48}{7}}}  \\ F_C=F(2,0)=2·2+3·0=4 \end{array} \right\} $

El valor máximo que alcanza la función $z=f(x,y)=2x+3y$, sujeta a las restricciones dadas, es $z_B={\large{\frac{48}{7}}}$ y se alcanza en el punto $B=\left({\large{\frac{6}{7}}},{\large{\frac{12}{7}}}\right)$, es decir, para los valores $x={\large{\frac{6}{7}}}, y={\large{\frac{12}{7}}}$.

La solución aplicando el método gráfico la puedes ver en el siguiente apartado curvas de nivel, tienes un enlace a geogebra para ver el proceso.

Rectas de nivel. 
Maximiza la función $z=f(x,y)=2x+3y$, sujeta a las restricciones:

$\left. \begin{array}{l} 3x+2y \le 6 \\ x+3y \le 6 \\ x \geq 0 \\ y \geq 0 \end{array} \right\} $

Construcción dinámica realizada con el programa GeoGebra. Sabemos que la solución de un problema de programación lineal está en una recinto concreto, su región factible, es importante; pero en esa región sigue habiendo una infinidad de puntos. Probar todas esas posibilidades es tarea imposible, se necesita algún resultado más contundente. Afortunadamente lo hay, pues: “La solución óptima de un problema de programación lineal se encuentra siempre en la frontera de la región factible. En particular, una solución óptima se halla en alguno de los vértices de esa región”.
Observa cómo el deslizador k de GeoGebra, conforme va tomando valores, la recta señalada en rojo va trasladándose paralelamente a la dirección determinada por la Función Objetivo $2x+3y=k$ (=Rectas de nivel). Estas rectas al interceptar el recinto convexo lo hacen siempre, tanto en el primer instante como en el último, en un vértice o en una arista de dicha región. Lo vemos en el siguiente enlace que muestra dicha construcción dinámica.
El proceso que observas en geogebra es ir aumentando y disminuyendo los valores de k en la función objetivo $2x+3y=k$, como puedes comprobar se trata de dibujar muchas rectas paralelas porque los coeficientes de x y de y son los mismos siempre (los de la función objetivo) y al desplazarnos sobre el recinto de soluciones factibles podemos ver cuales son los puntos del recinto que nos proporcionarán el máximo y el mínimo.
En este caso el mínimo es el punto $(0,0)$ porque es el que la curva de nivel (recta de la función objetivo) queda más a la izquierda, cualquier punto a su izquierda se sale del recinto de soluciones factibles, mientras que el máximo es el punto $\left({\large{\frac{6}{7}}},{\large{\frac{12}{7}}}\right)$ porque es el que nos proporciona la recta paralela a la función objetivo que queda más a la derecha, cualquier punto a la derecha de éste, se sale del recinto de soluciones factibles.