2. Comenzamos la programación lineal
1. Sistemas de inecuaciones
Antes de comenzar de lleno con la resolución de los ejercicios y problemas de programación lineal, hemos de recordar como representar un sistema de inecuaciones, ya que es necesario para poder resolver este tipo de problemas. En cualquiera de los métodos que vamos a ver en esta situación de aprendizaje tendremos que representar un sistema de inecuaciones.
Definición. Una inecuación lineal con dos variables es una expresión que se puede escribir en una de las siguientes cuatro formas:
$ \begin{array}{l} ax+by\leq c \\ ax+by < c \\ ax+by\geq c \\ ax+by > c \end{array} $
Para nuestros objetivos, sólo usaremos las desigualdades no estrictas:
$ \begin{array}{l} ax+by\leq c \\ ax+by\geq c \end{array} $
Aunque en realidad podemos expresar una desigualdad cualquiera con el signo que deseemos, gracias a la propiedad:
$ax+by\leq c\to -ax-by\geq -c$.
Su representación gráfica. A partir de la gráfica de una recta $y=mx+n$, podemos considerar las dos regiones (semiplanos) en que esta divide al plano. Como los puntos de estas regiones no verifican la ecuación de la recta, sucederá que $y\neq mx+n$. Por tanto, deberá ser entonces $y< mx+n$ o $y> mx+n$. Además, dos puntos de un mismo semiplano han de satisfacer la misma desigualdad ya que de lo contrario, existiría un punto intermedio entre ambos que debería verificar la igualdad y, por tanto, pertenecer a la recta separando a aquellos dos puntos en dos semiplanos distintos en contra de la hipótesis.
Método. Una vez representada la recta asociada a la inecuación, procedemos a determinar qué semiplano le corresponde. Para ello, podemos elegir un punto ensayo, por ejemplo, el O=(0,0), siempre y cuando el punto O=(0,0) no pertenezca a la recta de separación entre los dos semiplanos, y sustituimos sus coordenadas x=y=0 en la inecuación. No obstante, cualquier otro punto puede servir como punto de ensayo, pero elegimos este al resultar más sencillo la sustitución en cualquier inecuación. Si se verifica la desigualdad, entonces todos los puntos que se encuentran en el mismo semiplano que el O=(0,0) también la verificarán. En caso contrario, será el otro plano, conjunto solución de la inecuación dada.
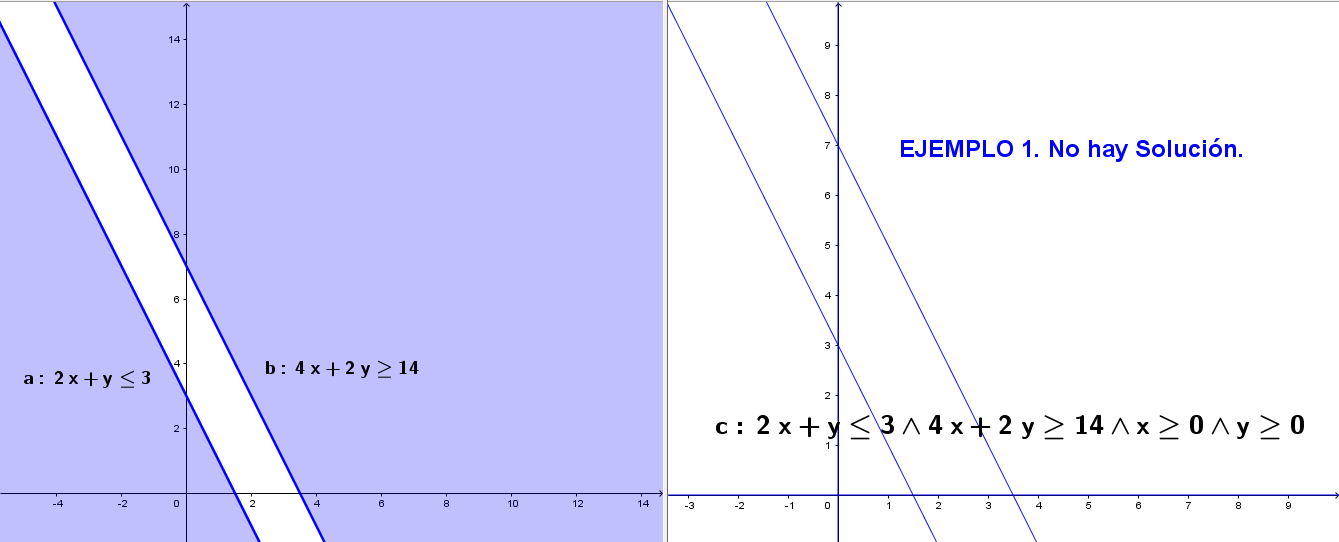
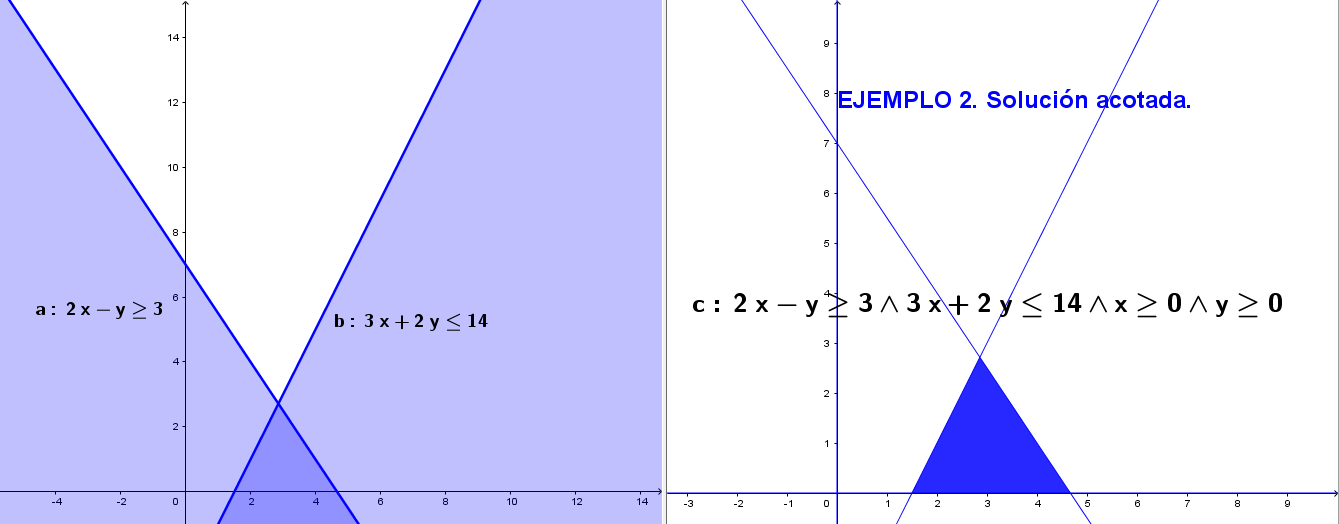
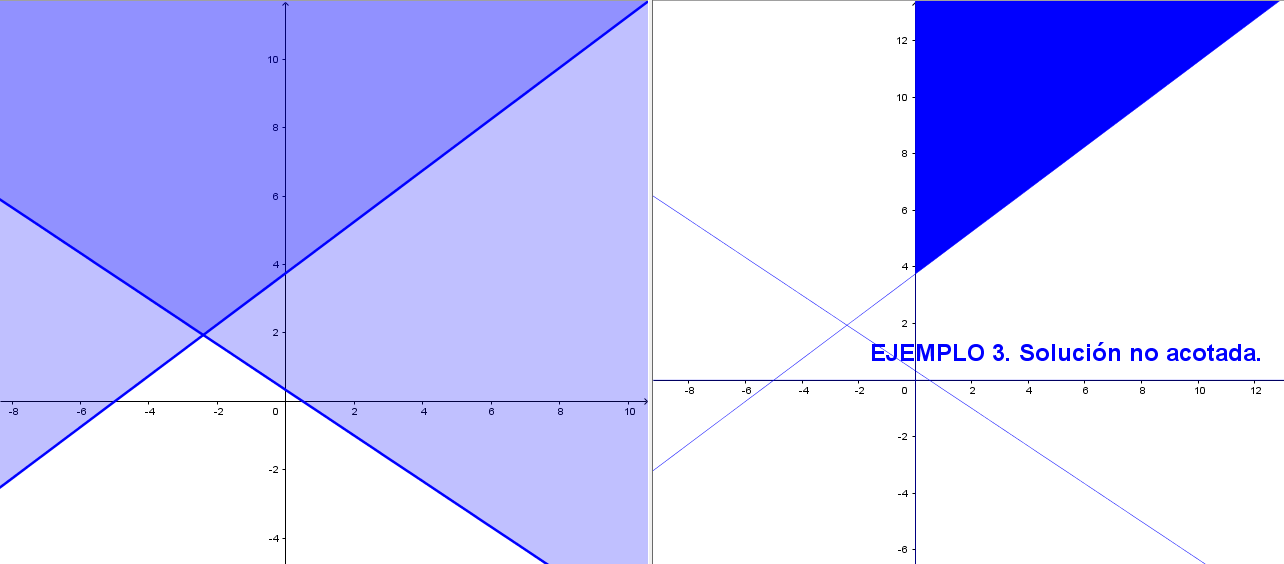
Sistema. Actuamos de una manera ordenada para cada una de las restricciones o desigualdades que forman el sistema dado. Aquella región cuyos puntos verifiquen todos y cada una de las desigualdades formarán el conjunto solución. La intersección de los semiplanos asociados determinarán el conjunto solución. Este conjunto solución puede ser vacío (Ejemplo 1), acotado (Ejemplo 2) y no acotado (Ejemplo 3).
A las restricciones particulares y propias de cualquier sistema, añadiremos dos más de cara a la Resolución de Problemas de Programación Lineal. Estas restricciones generales estarán siempre presentes y serán $x\geq 0; y\geq 0$ (no negatividad de las variables).
Utiliza el siguiente recurso de GeoGebra para practicar con distintos ejemplos que tú mismo podrás implementar.
2. Protocolo de actuación
Protocolo a seguir. Sea este mi primer acercamiento a un problema de Programación Lineal. La resolución de un problema de un modelo de programación lineal implica encontrar los valores de las variables de decisión que maximizan o minimizan una función objetivo sujeta a un conjunto de restricciones lineales. Aquí hay algunos pasos básicos que puedes seguir para resolver un problema de programación lineal:
1. Definición de n variables de decisión: Identifica las variables que representarán las decisiones que quieres tomar en tu problema. Asigna letras a estas variables. Por ejemplo si son dos, $x,\ y$ y si son más de dos, $x_1,\ x_2,\ ...,\ x_n$.
2. Formulación de la función objetivo: Define la función objetivo que deseas maximizar o minimizar en términos de las variables de decisión. Asigna un coeficiente a cada variable en la función objetivo.
3. Establecimiento de restricciones: Identifica las restricciones que limitan las posibles soluciones. Expresa estas restricciones como ecuaciones o desigualdades lineales en términos de las variables de decisión.
4. Graficar las restricciones (n=2): Si estamos trabajando en un problema bidimensional, representamos gráficamente las restricciones en el plano cartesiano para así poder visualizar la región factible.
5. Identificación de los vértices de la región: Halla los puntos de intersección de las restricciones para obtener así los vértices de la región factible.
6. Evaluación de la función objetivo en los vértices: Calcula el valor de la función objetivo en cada vértice de la región factible.
7. Selección de la solución óptima: Determina qué vértice produce el valor máximo o mínimo de la función objetivo. Esta será tu solución óptima. Puede ocurrir que dos vértices consecutivos presenten el mismo valor óptimo (importante: tienen que ser consecutivos), en ese caso cualquier punto adecuado del segmento que los une se puede considerar máximo. Punto adecuado se refiere a que si el problema trata de valores de x e y, que deben ser números naturales (son sillas y sillones, o cajas de dos tipos, en general elementos que no se pueden dividir), solo valdrán los puntos del segmento que cumplan esas condiciones.
8. Interpretación de la solución: Traduce la solución encontrada en términos del problema original.
Es importante señalar que estos pasos proporcionan una guía general y la complejidad de la resolución puede aumentar según la cantidad de variables y restricciones en el problema. Además, existen algoritmos computacionales específicos para resolver problemas de programación lineal de manera eficiente, como el método Simplex y el método Solver. Estos métodos son especialmente útiles para problemas más complejos.
Ejemplo. Un pastor suministra a sus ovejas dos tipos de piensos con el contenido vitamínico (mg/k) miligramos por kilo que muestra la tabla:
| A1 | A2 | |
| Pienso Tipo 1 | 3 | 5 |
| Pienso Tipo 2 | 4 | 2 |
Se desea suministrar diariamente al menos 5 mg de la vitamina A1 y 7 mg de la vitamina A2. El precio del kilo de pienso del tipo 1 es de 0’5 €, y el kilo de pienso del tipo 2 de 0’6 €. Se promueve hacer una mezcla que se ajuste a estas condiciones y resulte lo más económica posible.
Plantea el Programa Lineal y resuélvelo.
Resolución. Sigamos el protocolo de actuación en este ejemplo.
| Protocolo de actuación en un problema de Programación Lineal (n=2 variables) | ||
| 1. Variables de decisión: |
$x=$ número de kilos del pienso de Tipo 1 |
$x,\ y$ |
| 2. Función Objetivo: | El precio del kilo de pienso del tipo 1 es de 0'5 euros, y el kilo de pienso del tipo 2 de 0'7 euros. | $z=F(x,y)=0'5·x+0'6·y$ (Mínimo) |
| 3. Establecimiento de restricciones: | Se desea suministrar diariamente al menos 5 mg de la vitamina A1 y 7 mg de la vitamina A2. |
$\left. \begin{array}{l} 3x+4y\geq5 \\ 5x+2y\geq7 \\ x \geq 0 \\ y \geq 0 \end{array} \right\} $ |
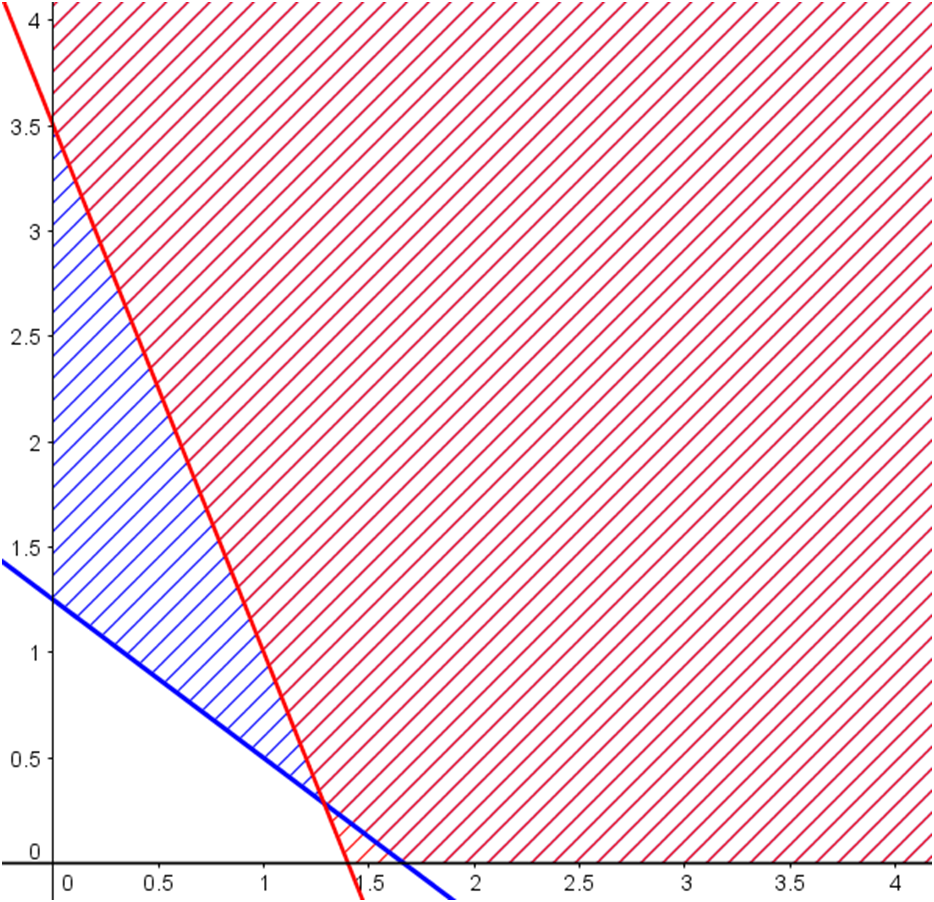
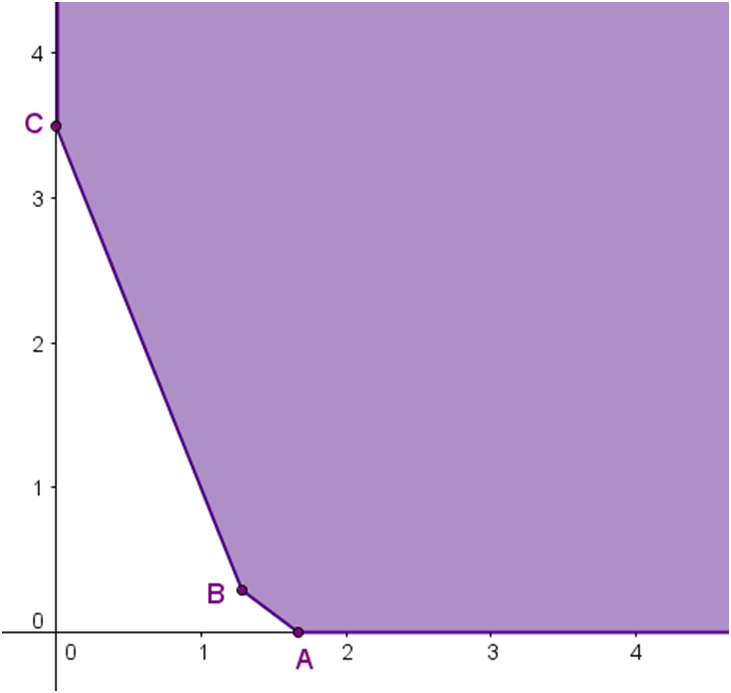
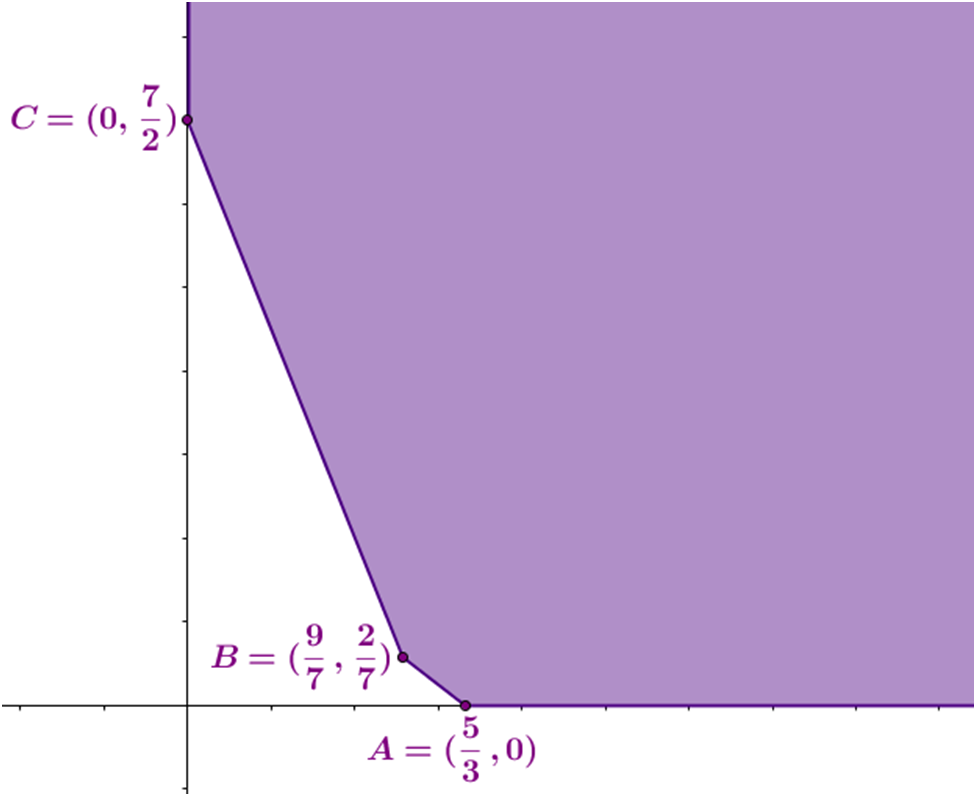
| 4. Graficamos las restricciones: |
|
|
| 5. Identificación de los vértices de la región: |
Los vértices de esta Región Factible No Acotada son: $A=\left(\frac{5}{3},0\right)$ $B=\left(\frac{9}{7},\frac{2}{7}\right)$ $C=\left(0,\frac{7}{2}\right)$ |
|
| 6. Evaluación de la función objetivo en los vértices: |
$z_A=F\left({\large{\frac{5}{3}}},0\right)=0'5·{\large{\frac{5}{3}}}+0'6·0={\large{\frac{5}{6}}}$ |
$z_A={\large{\frac{5}{6}}}$ |
| 7. Selección de la solución óptima: |
$z_A={\large{\frac{5}{6}}}\cong 0'83$ |
$z_B={\large{\frac{57}{70}}}\cong 0'81$ (Valor Mínimo) |
| 8. Interpretación de la solución: |
Con los aportes vitamínicos A1 y A2 que deben ser aportados, la dieta más económica sería la que mezclase ${\large{\frac{7}{9}}}\cong 0'77$ kilos del pienso Tipo 1 con ${\large{\frac{2}{7}}}\cong 0'29$ kilos del pienso Tipo 2. De esta forma, resultaría una mezcla por un valor de ${\large{\frac{57}{70}}}\cong 0'81€$. |
|