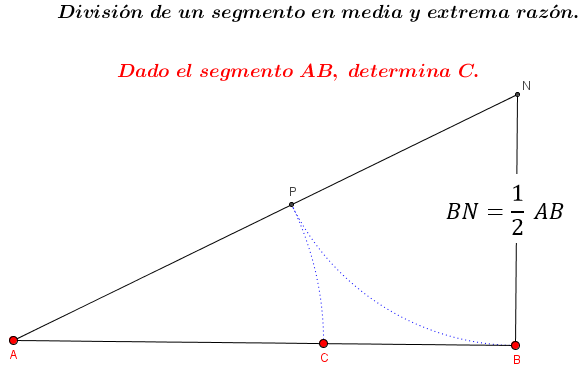
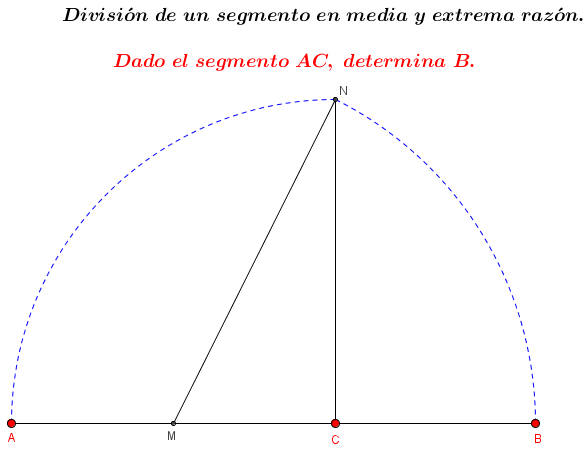
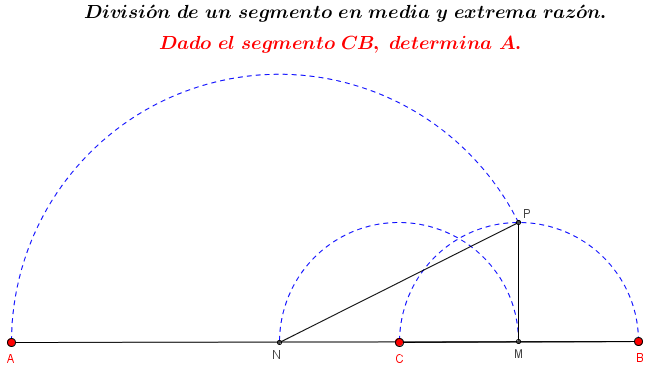
1. Aprenderemos ahora los conceptos de Razón y Proporción
RAZONAMIENTO PROPORCIONAL: el razonamiento proporcional supone pensar en las relaciones y hacer comparaciones entre dos o más cantidades usando el razonamiento multiplicativo. Se requiere que pensemos en números y valores en términos relativos, en lugar de absolutos. El razonamiento proporcional constituye una parte muy importante de las matemáticas básicas, ya que sustenta muchos otros temas. Por ejemplo, resulta fundamental para trabajar con fracciones, decimales y porcentajes, así como con semejanzas y ampliaciones. El razonamiento proporcional también sirve de ayuda cuando se trabajan otros temas de matemáticas, desde la simple probabilidad hasta problemas que involucran la trigonometría. Además, el razonamiento proporcional tiene muchas aplicaciones prácticas en la vida cotidiana. Se puede utilizar para calcular las mejores compras, para trabajar con dibujos y mapas a escala, para ajustar recetas o crear concentraciones particulares de mezclas y soluciones y para realizar conversiones de moneda.
RAZÓN: en el tema anterior sobre el concepto de fracciones y números racionales, hemos visto que entre los usos de las fracciones figura el de razón, entendida como la comparación entre una parte y otra parte. Es importante, sin embargo, estudiar con más detalle el uso que se hace del término razón, ya que no siempre es sinónimo de fracción. La idea clave es que las fracciones son cualquier par ordenado de números enteros cuya segunda componente es distinta de cero, mientras que una razón es un par ordenado de cantidades de magnitudes. Cada una de esas cantidades vienen expresadas mediante un número real y una unidad de medida. El hecho de que en las razones se refieran a cantidades de magnitudes, medibles cada una con sus respectivas unidades, implica las siguientes diferencias con las fracciones:
- Las razones comparan entre sí objetos heterogéneos, o sea, objetos que se miden con unidades diferentes. Por ejemplo, 4 paquetes de arroz por 12 euros. Las fracciones, por el contrario, se usan para comparar el mismo tipo de objetos como 1 de 3 partes, lo que se indica con 1/3. Según esto la razón 4 paquetes/12 euros no es una fracción.
- Algunas razones no se representan como una fracción. Por ejemplo, 80 Km/hora. En este caso no se usa la notación de fracción para informar de la relación entre dichas cantidades.
- Se pueden designar de un modo distinto al de las fracciones. La razón 4 a 7 se puede poner como 4:7.
- En las razones, el segundo componente puede ser cero. En una urna de bolas de distintos colores la razón de bolas verdes a rojas puede ser 3:5, pero también se puede decir que puede ser 3:0, si es que todas son verdes (no se trata de hacer ninguna división por 0).
- Las razones no son siempre números racionales. Por ejemplo, la razón de la longitud de una circunferencia a su diámetro $\frac{L}{D}=\pi$, que sabemos no es racional.
- Las operaciones con razones no se realizan, en general, de igual manera que las fracciones. Por ejemplo, 2 aciertos sobre 5 intentos (2:5), seguidos de 3 aciertos sobre 7 intentos (3:7) se combinan para producir 5 aciertos en un total de 12 intentos, o sea, con estas fracciones se puede definir una suma de razones del modo 2:5 + 3:7 = 5:12. Evidentemente esta suma no es la misma que la suma de fracciones $\frac{2}{5}+\frac{3}{7}\neq\frac{5}{12}$.
PROPORCIÓN: una proporción aparece en general bajo la forma de una igualdad entre dos razones. En consecuencia, el producto cruzado de los numeradores y denominadores serán iguales entre sí. Cualquier cambio de disposición entre los cuatro números que forman una proporción que no modifique los productos cruzados de los numeradores y denominadores entre sí dará lugar a una nueva igualdad de fracciones. Una proporción permite por tanto, escribir cuatro igualdades equivalentes entre dos fracciones como vemos a continuación:
$\frac{a}{b}=\frac{c}{d};\frac{b}{a}=\frac{d}{c};\frac{a}{c}=\frac{b}{d};\frac{c}{a}=\frac{d}{b};$
En la práctica, una de las fracciones tendrá el numerador o el denominador desconocido y se planteará el problema de hallar su valor usando la relación de proporcionalidad establecida.
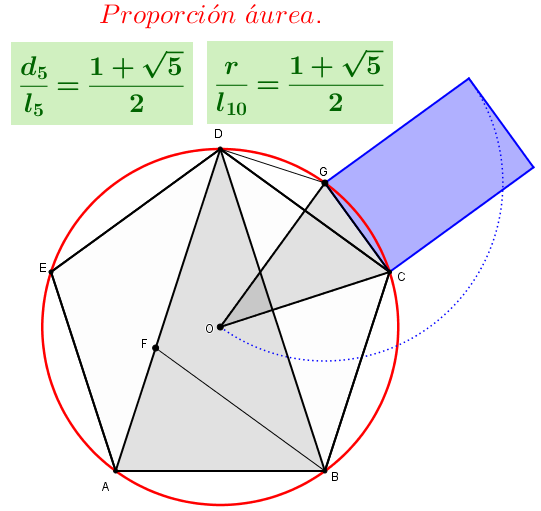
LA PROPORCIÓN en el arte representa uno de los aspectos más clásicos y evidentes en relación con la Geometría. Todos hemos oído hablar de obra “bien proporcionada” o de que tiene “unas buenas proporciones”, sin pararnos a pensar en el significado preciso de estas frases. Si una proporción es la razón entre dos medidas. ¿Qué medidas hemos de considerar de una obra de arte? Lo sencillo es comenzar por las formas rectangulares más o menos definidas y determinar la proporción entre la medida del lado mayor y el lado menor del rectángulo. Esto nos lleva a la consideración y estudio de ciertos rectángulos y proporciones notables por su extendido uso. Es la proporción áurea o divina proporción, Φ(Fi), la que ha marcado el mayor canon estético en el arte y arquitectura a lo largo de la historia (Fig. 1). Se tienen noticias de su uso bastante antes de que Euclides en sus Elementos hiciese un tratado geométrico de ella, pues parece ser que en el templo de Andros descubierto en Las Bahamas ya se había usado (hace unos diez mil años). La proporción áurea puede considerarse como uno de los ejemplos más claros de modelo geométrico aplicado al arte. Una vez estudiadas sus cualidades geométricas se idealiza como canon estético. Su estrecha relación con el pentágono regular (Fig. 2) y con la sucesión de Fibonacci, que a su vez reflejan modelos de forma y crecimiento en la Naturaleza (Haz Clic), agrandan aún más esta idealización de forma que tal proporción es considerada mas bien como un descubrimiento de una cualidad universal divina que una creación humana.
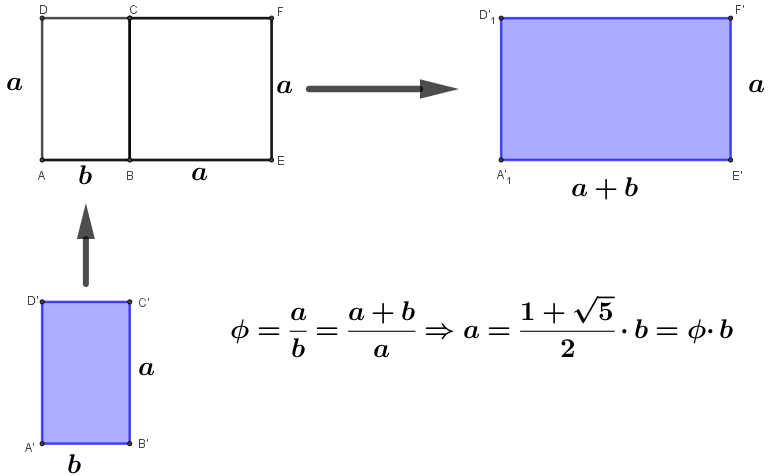
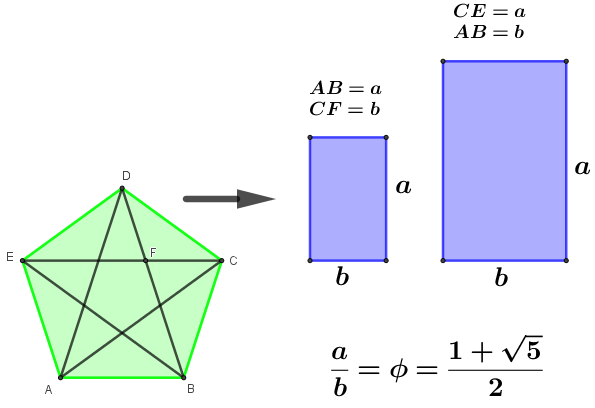
Es bien conocida la proporción áurea y su extendido uso en la Grecia antigua y su redescubrimiento en el Renacimiento, pero podemos encontrarla también en el arte de otras épocas y estilos, de forma más o menos directa con la utilización de rectángulos en dicha proporción, líneas de horizontes en cuadros y fotografías para dividir así la longitud total de la reproducción en tal proporción. La proporción de un rectángulo determina y queda determinada por la inclinación de las diagonales. Rectángulos de la misma proporción y que tengan los lados paralelos tienen las diagonales paralelas dos a dos o, perpendiculares dos a dos. Si usamos esta idea (que se desprende de las leyes de la semejanza) podemos localizar rectángulos de una determinada proporción usando un cartabón especial construido con los catetos en tal proporción y haciendo un barrido paralelo sobre la reproducción plana (dibujo, fotografía, plano, etc.)
Aunque la idealización del rectángulo áureo ha hecho que aparezca no sólo en la Arquitectura y demás Artes, sino también en el formato de objetos tan cotidianos como las tarjetas de crédito o los carnets de identidad. No ha sido, por supuesto, la única proporción usada. Cada rectángulo, áureo o no, marca un patrón de crecimiento caracterizado por el mantenimiento de la proporción. Cada uno necesita de una figura diferente a añadir para que se obtenga otro semejante, lo que los griegos llamaron gnomon. El gnomon de un rectángulo de oro es un cuadrado, el de un rectángulo $\sqrt{2}$, el de los famosos formatos DIN de papel, es otro rectángulo idéntico. En general, el trazado geométrico para obtener a partir de un rectángulo el gnomon y el siguiente rectángulo semejante está basado en la idea de la perpendicularidad de diagonales que hemos comentado anteriormente.
LA PROPORCIÓN ÁUREA:
(...) Pero es imposible combinar dos cosas sin una tercera: es preciso que exista entre ellas un vínculo que las una. No hay mejor vínculo que el que hace de sí mismo y de las cosas que une un todo único e idéntico. Ahora bien, tal es la naturaleza de la proporción áurea (…)
Platón, Timeo
El número de formas distintas de dividir una figura es, naturalmente, infinito, pero la sección áurea produce una impresión de armonía lineal, de equilibrio en la desigualdad, más satisfactoria que la de cualquier otra combinación, según los cánones de belleza de la Grecia clásica, que posteriormente fueron seguidos por Leonardo da Vinci y la mayor parte de los artistas del Renacimiento. Tras este periodo, el estudio de la sección áurea cayó después en el olvido durante más de dos siglos, pese a que numerosos autores emplearon esta proporción en sus obras, hasta que el alemán Adolf Zeysing, en el año 1854, volvió a destacar sus propiedades estéticas y proclamó: “Para que un todo, dividido en partes desiguales, parezca hermoso desde el punto de vista de la forma, debe haber entre la parte menor y la mayor la misma razón que entre la mayor y el todo”. Zeysing nombró esta formulación como “ley de las proporciones”, afirmando que se cumple en las medidas ideales del cuerpo humano, de las especies animales que se distinguen por la elegancia de sus formas, en ciertos templos griegos (particularmente el Partenón), en botánica y hasta en la música. Un ejemplo de la presencia de esta medida para el estudioso alemán sería el hecho de que en las estatuas antiguas y en las personas perfectamente proporcionadas, el ombligo divide la altura total mediante la proporción áurea. El propio Zeysing realizó mediciones sobre miles de cuerpos humanos y se encontró con que este canon ideal parece ser la expresión de una ley estadística media para los cuerpos sanamente desarrollados. Esta proporción, que está de acuerdo con los cánones de Durero y de Leonardo, fue comprobada nuevamente en las estatuas griegas de la época de Fidias. Al operar sobre estas series de observaciones, Zeysing observó y constató que las proporciones del cuerpo masculino oscilan en torno a la razón media $\frac{m}{n}=\frac{13}{8}=1.625$, obteniendo un resultado ligeramente inferior a la sección áurea para las mismas proporciones del cuerpo femenino, en el cual se verifica que el valor de la razón media es $\frac{m}{n}=\frac{8}{5}=1.6$. En cualquier caso, a partir de este estudio empírico, tanto sobre cuerpos reales como sobre obras escultóricas clásicas, se llega a la consideración de la proporción áurea como símbolo de la perfección estética.
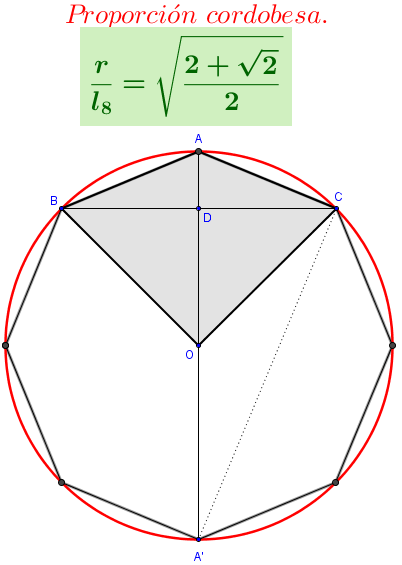
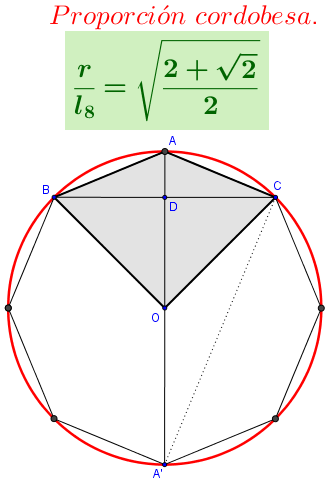
LA PROPORCIÓN CORDOBESA:
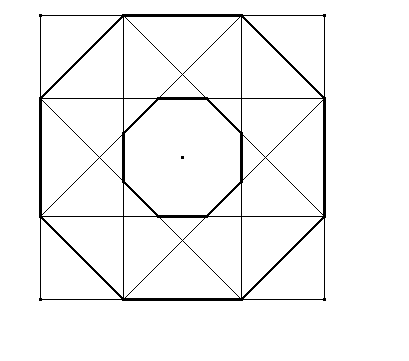
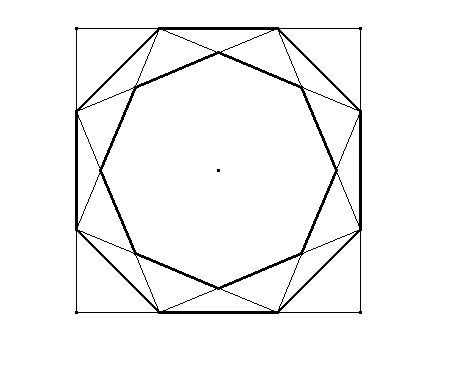
El arquitecto cordobés Rafael de la Hoz detectó un abundante uso de otra proporción en la arquitectura local andaluza. Sus estudios, de carácter empírico, mostraron el uso de una proporción con un valor aproximado 1’3. La proporciones notables $\Phi, \sqrt 2,\sqrt3$ están relacionadas con distintos polígonos regulares como el pentágono y decágono en el caso de $Phi$, con el cuadrado en el caso de $\sqrt2$ y con el triángulo equilátero en el de $\sqrt3$. Dado que la razón entre el radio de una circunferencia y el lado del octógono regular inscrito es $\frac{1}{\sqrt{2-\sqrt2}}=1'306...$, parecía lógico enmarcar el valor empírico 1’3 en dicho valor teórico; y así lo hace Rafael de la Hoz, llamando Proporción Cordobesa a la razón entre el radio y el lado del octógono regular. La presencia de esta proporción está más que justificada en el Arte Islámico ya que está repleta de cuadrados y octógonos regulares. La decoración basada en temas geométricos trae como consecuencia la creación prolífica de mosaicos y frisos que cubran las distintas superficies de los edificios. La decoración es esencial en el Arte Islámico. Mientras que en el arte occidental tiene un valor secundario, en el islámico juega un papel central. En occidente lo ornamental se aplica como adorno de la estructura del edificio, que es lo primordial. En las artes del Islam, la decoración llega a enmascarar los materiales constructivos. Lo invade todo.
Las Matemáticas en el Arte islámico: Los motivos geométricos.
La geometría es muy importante en el Islam. A través de ella se representa la indivisibilidad de Dios. La forma perfecta es el círculo. Se utiliza como patrón que permite crear otros motivos. El diseño es sencillo, se aplican los principios de repetición simétrica, multiplicación o subdivisión. Se trata de un arte más intelectual que emocional, de base matemática. Se utilizan ramas mixtilíneas entrecruzadas formando rombos, cintas trenzadas, meandros, dibujos en zigzag, ajedrezados y lazos formando estrellas. El mocárabe o mucarna es la decoración de prismas, yuxtapuestos y dirigidos hacia abajo, que acaban en un estrechamiento llamado prismático, cuya superficie inferior es cóncava. Se emplea especialmente en la arquitectura.
Destacan entre ellas, las ciudades de Granada (Arte Nazarí) y Córdoba. Sus principales obras arquitectónicas como la Alhambra y la Mezquita, constituyen un extenso reflejo de ello. Andalucía posee un enorme patrimonio artístico y cultural que debe, en gran parte, a los musulmanes. En efecto, se considera Al-Ándalus (711-1492), la época de máximo esplendor del sur de España. El Islam dejó una huella muy importante en la cultura hispánica, en la música, la cocina, la lengua, pero, sobre todo, en la arquitectura. Y no hay mejor forma de descubrirlo que visitando los monumentos musulmanes más importantes de nuestra región y observándolos con unas lentes matemáticas. Este debería ser también uno de los objetivos en este tema.