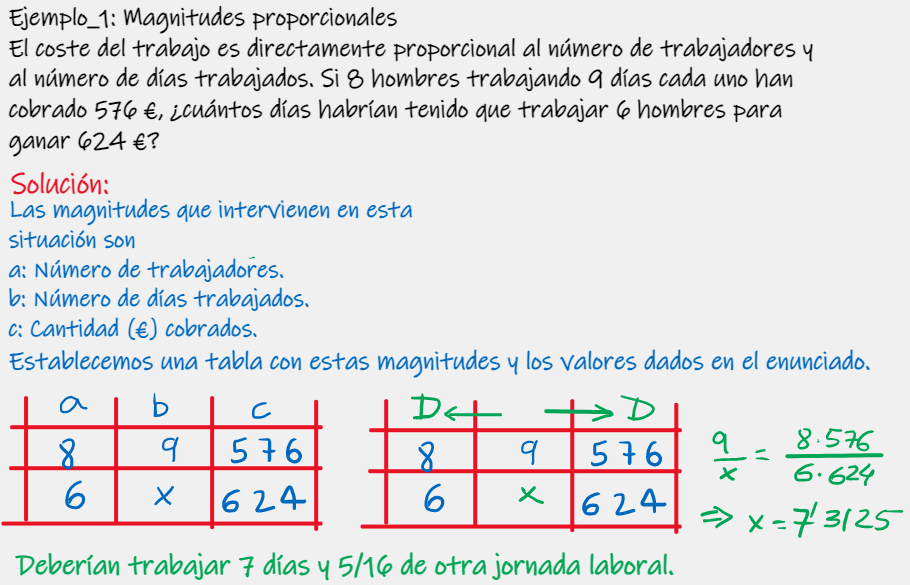
1. Repasamos los tipos de proporcionalidad
PROPORCIONALIDAD SIMPLE.
La proporcionalidad directa se produce cuando los valores de dos magnitudes aparecen a la vez, multiplicados o divididos por un mismo número. Al dividir cualquier valor de una de las magnitudes por su valor correspondiente de la otra magnitud, siempre se obtiene el mismo valor (constante), esta constante se llama razón de proporcionalidad directa. Ejemplo ilustrativo de dos magnitudes x, y, que están en proporcionalidad directa.
| Magnitudes | Valores | Constante de Proporcionalidad | Expresión funcional | Gráfica |
| x | {1,2,3,4,...,x,...} | $k=\frac{y}{x}$ |
$y=kx$ |
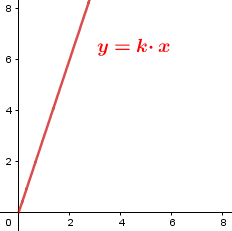 |
| y | {3,6,9,12,...,3x,...} |
La proporcionalidad inversa se produce cuando el producto de los valores correspondientes de dos magnitudes es constante. Como consecuencia, dos magnitudes son inversamente proporcionales cuando al multiplicar (dividir) una cantidad de la primera magnitud, la cantidad correspondiente de la segunda magnitud queda dividida (multiplicada) por dicho número. Ejemplo ilustrativo de dos magnitudes x, y, que están en proporcionalidad inversa.
| Magnitudes | Valores | Constante de Proporcionalidad |
Expresión funcional |
Gráfica |
| x | {3,6,9,12,...,x,...} | $k=x·y$ | $y=\frac{k}{x}$ | 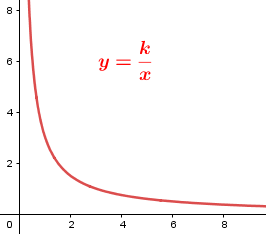 |
| y | {12,6,4,3,...,$\frac{36}{x}$,...} |
PROPORCIONALIDAD COMPUESTA.
Supongamos ahora que en un mismo contexto de proporcionalidad intervienen un número de magnitudes mayor que dos. Por ejemplo, si la magnitud $y$ varía en razón inversa a $x$ y en razón directa a la magnitud $z$, esto significará que $y=\frac{k·z}{x}$. En este otro caso, $y=\frac{k·x_1·x_2}{x_3·x_4}$, diremos que la magnitud $y$ es directamente proporcional a las variables $x_1$ y $x_2$ e inversamente proporcional a las variables $x_3$ y $x_4$.