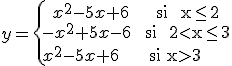2.2. El valor absoluto
Como ya sabemos, el valor absoluto transforma en positivo un número negativo y lo deja positivo si es positivo. Así, en una función f(x), si construimos la función g(x) = |f(x)|, ésta se queda igual en el trozo donde la función es positiva (está por encima del eje OX) y se lleva a positiva todo el trozo donde la función es negativa (por debajo del eje OX) como si se doblara la gráfica por el eje OX.
Observa la siguiente escena para ver cómo se construye la gráfica del valor absoluto de una gráfica cualquiera. En la barra de entrada inferior puedes ir cambiando la función y cuando lo hagas le das a la tecla "entrar" :
Escena de José Luis Alonso Borrego en Proyecto Descartes. Licencia CC
Comprueba lo aprendido
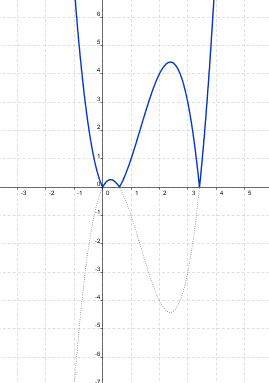
Cógete papel y lápiz y haz las gráficas del valor absoluto de las funciones cuyas gráficas son las siguientes:
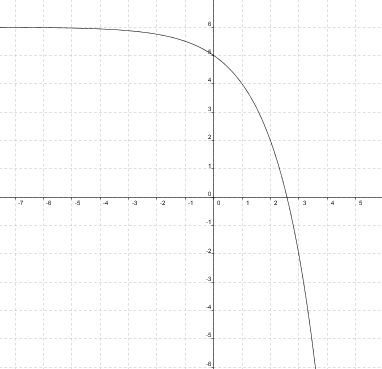
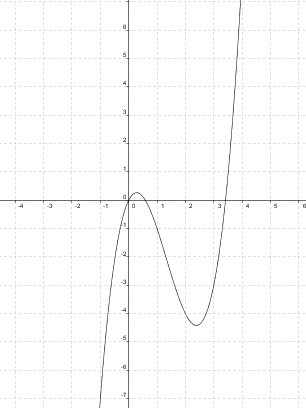
Las gráficas deben haberte salido similares a estas:
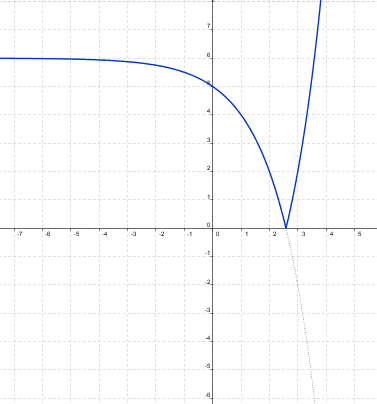 |
 |
Acabamos de ver cómo actúa el valor absoluto sobre la gráfica de una función. Vamos ahora a transformar el valor absoluto de una función en una función a trozos, y lo vamos a hacer sobre la más simple, sobre f(x) = |x|
Ya sabemos, que el valor absoluto deja lo positivo como positivo y lo negativo lo transforma en positivo.
Por tanto, si x es positivo (x>0) el valor absoluto de x seguirá siendo x, o sea, |x|=x
Por otro lado, si x es negativo (x<0) el valor absoluto de x lo cambiará de signo y será así -x, luego, |x|=-x
Y si x = 0, pues seguirá siendo 0 el valor absoluto, o sea, que igual lo podemos poner en cualquiera de las dos desigualdades.
Si lo escribimos como una función a trozos, tendremos que:
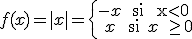
y su gráfica será:
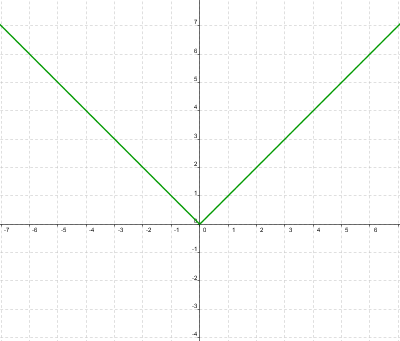
Ejercicio Resuelto
Vamos a transformar en funciones a trozos las siguientes funciones que vienen dadas por valores absolutos:
La primera, f(x) = |2x+4|
Como segundo ejemplo, vamos a transformar en función a trozos la función y = |-3x + 1|
Comprueba lo aprendido
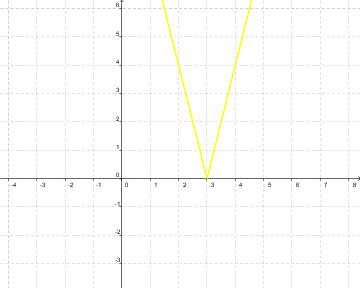
Transforma a trozos la función y = | 4x - 12 | y haz su gráfica.
La función a trozos debe salirte así:
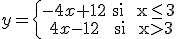
Y su gráfica:
Para saber más
Si tenemos otro tipo de función la forma de pasarla a trozos es similar. Únicamente varía la forma de transformar los dominios.
Por ejemplo, si tenemos y = |x2 - 5x + 6|, empezamos igual:
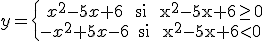
Ahora, para ver esa inecuación x2-5x+6<0, resolvemos la ecuación x2-5x+6=0 (aplicando la fórmula) y obtenemos como resultado 2 y 3.
Hacemos una tabla y vemos los signos de la función en cada intervalo:
| (-∞ , 2) | (2 , 3) | (3 , + ∞) |
| + | - |
+ |
Para completar los signos, le hemos dado un valor a x dentro de ese intervalo, lo hemos sustituido en la función y hemos visto el signo del resultado.
Entonces nuestra función a trozos queda: