1.3 Estimaciones con las rectas de regresión

Pues ya que tenemos todo lo necesario. Vamos a aplicar todo lo que hemos aprendido en este tema a situaciones reales.

La utilidad de la recta de regresión es que nos permite predecir valores que se van a dar en una variable cuando le damos un valor que no conocemos a la otra. Además, con el coeficiente de correlación, podemos saber si la predicción que estamos haciendo es buena o no, si es fiable o no lo es.

En el siguiente importante, puedes ver los pasos a seguir para resolver un problema de regresión lineal:

Importante

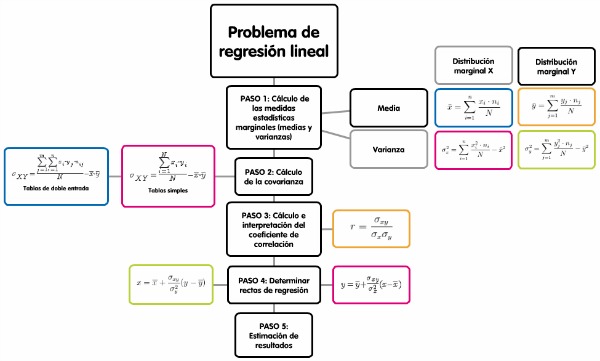
Con el siguiente gráfico puedes realizar un rápido repaso por todo lo visto en el tema:

Imagen de elaboración propia. Haz clic en la imagen para ampliar

En el siguiente vídeo puedes ver un ejercicio completo de regresión lineal siguiente los pasos descritos en el Importante anterior:

Vídeo de lasmatematicas.es alojado en Youtube

Caso práctico

En uno de los informes sobre estadísticas hospitalarias, Mercedes observa la evolución de las donaciones de sangre en Andalucía. Parece evidente que la concienciación social y la solidaridad de la población sobre este asunto es cada vez mayor.

Con el objeto de analizar de manera rigurosa la evolución de las donaciones de sangre y de hacer una estimación de lo que ocurrirá en años venideros, se ha recogido en la siguiente tabla la Tasa de donaciones de sangre (n.º de donaciones por cada 1000 habitantes) en Andalucía desde el año 94 hasta 2008:

Año	1994	1995	1996	1997	1998	1999	2000	2001	2002	2003	2004	2005	2006	2007	2008
Tasa de donaciones	31,70	32,40	33,10	3,10	32,50	34,66	34,62	35,00	35,30	34,94	35,18	33,62	33,30	32,88	34,08

¿Qué tasa de donaciones se prevé que haya en el año 2009? ¿Y en 2010? ¿Cómo son de fiables estas predicciones?

Retroalimentación

En primer lugar, vamos a ponerle nombre a las variables. Aunque daría lo mismo, parece lógico llamarle X al año e Y a la tasa de donaciones. Así, tenemos:

X = año en curso

Y = tasa de donación anual.

Como queremos estimar un valor de la variable Y conocido uno de X, hemos de calcular la recta que me da valores de Y en función de los de X, o sea, la recta de regresión de Y sobre X.

Al igual que en los ejemplos que había que calcular el coeficiente de correlación, lo primero es sacar la media y la desviación típica de cada variable por separado. Así comenzamos sacando la distribución marginal de ambas y el cálculo de los dos parámetros.

Ahora ya sí tenemos todo lo necesario para calcular la recta de regresión. Así, aplicamos la fórmula y sustituimos los valores de arriba:

Ahora sólo es cuestión de realizar los cálculos y simplificar la expresión:

Luego la recta de regresión de Y sobre X es:

Y= 0,0782·x - 122,719

Nos piden que estimemos el valor de la tasa de donaciones para el año 2009 y 2010. Pues bien, únicamente hemos de sustituir "x" por esos valores y calcular el valor de Y.

Año 2009: Y = 0,0782·2009 - 122,719 = 34,3848; o sea, 34,38 donaciones por cada 1000 habitantes de Andalucía.

Año 2010: Y = 0,0782·2010 - 122,719 = 34,463; o sea, 34,46 donaciones por cada 1000 andaluces.

Nos queda contestar acerca de la fiabilidad de estas predicciones, y esta información nos la da el coeficiente de correlación.

Así que como puedes ver, la correlación es débil o muy débil, por lo que las predicciones no son demasiado fiables.

En este segundo ejemplo, se está haciendo un estudio de control de población de conejos y zorros en una zona de bosque. Se cree que el número de ambas especies está íntimamente relacionado.

Durante los últimos 8 años se ha hecho un censo de ambos animales, obteniéndose las cifras que se muestran a continuación:

N.º zorros	20	30	15	20	26	30	15	14
N.º conejos	320	500	270	310	400	450	200	250

¿Cuántos zorros deberá haber si en el último año se han contado 350 conejos? Y si un año llegaran a contarse 1000 conejos, cuántos zorros debería haber para que el ecosistema fuera sostenible? ¿Son fiables las predicciones?

Retroalimentación

Igual que antes, debemos comenzar poniendo nombre a las variables. Por ejemplo vamos a llamar X al número de zorros e Y al número de conejos.

Si ahora nos piden una cifra de zorros sabiendo una de conejos, debemos calcular la recta que me da valores de zorros (X) a partir de los conejos (Y). Por tanto, ahora debemos calcular la recta de regresión de X sobre Y.

(Si la elección de incógnitas la hubiésemos hecho al revés, calcularíamos la otra recta)

Empezamos igual que en el ejemplo anterior; distribuciones marginales, medias y desviaciones.

Variable X

Variable Y

Covarianza

S_XY= 584,375.

Calculamos la recta de regresión de X sobre Y como ya hemos dicho antes. Aplicamos la fórmula y sustituimos los valores obtenidos:

Hacemos los cálculos y simplificamos la expresión:

Luego la recta de regresión de X sobre Y es:

X = 0,0622 · y + 0,26

Ahora ya, sí podemos hacer las predicciones que nos piden. Sólo tendremos que sustituir la "y" por el número de conejos que me den:

Hay 350 conejos: X = 0,0622·350 + 0,26 = 22,03; o sea, si hay 350 conejos debe haber 22 zorros.

Hay 1000 conejos: X = 0,0622·100 + 0,26 = 62,46; o sea, si hubiera 1000 conejos, debería haber 62 ó 63 zorros para que el sistema en el bosque se mantuviera.

Para la fiabilidad, nuevamente calculamos el coeficiente de correlación, aunque en este ejemplo hay truco:

Como podemos ver, la correlación entre las dos variables es muy fuerte, lo que hace que en principio, las predicciones sean muy fiables. En el primer caso está asegurado, pero en el segundo no tanto, pues en los datos recogidos, no hay ninguno que tan siquiera se acerque al valor de 1000 conejos, por lo que no tenemos ninguna información sobre el comportamiento de la población de zorros y conejos con esos datos. Por tanto, podemos decir que la primera estimación es muy fiable pero la segunda no tanto.

Para que la estimación sea buena, la correlación tiene que ser muy fuerte y el valor que queramos estimar debe estar comprendido entre los datos que hemos recogido.

Comprueba lo aprendido

Ahora te toca a ti. Vas a hacer un ejercicio en el que al final tienes que hace un pronóstico sobre aguas y cultivos.

Ve rellenando los distintos huecos. Si aparecen decimales, usa la coma para separar y redondea todos los resultados con 3 decimales, aunque si te equivocas en algún decimal tampoco ocurre nada.

El historial hidrológico de Olvera en los últimos 8 años y la producción de aceitunas que han dado los olivos del campo de Curro vienen dados por la siguiente tabla:

Año	2002	2003	2004	2005	2006	2007	2008	2009
L/m²	702	680	650	710	640	600	604	673
Producción ( miles kg)	215	220	184	221	168	136	162	197

Aunque en la cooperativa le informan a Curro de nuevos abonos que mejoran el rendimiento y de los distintos tipos de insecticidas que ha usado, Curro cree que el único factor determinante de la producción de sus olivos es el agua que cae en el año. ¿Tiene razón Curro y es verdad que la cantidad de agua es tan decisiva?
¿Qué cantidad de agua tendría que llover para que la producción fuera al menos de 250.000 kg de aceitunas?

Le llamamos X al agua caída e Y a la producción obtenida.

Media de X = Rellenar huecos (1): Desviación típica de X = Rellenar huecos (2):

Media de Y = Rellenar huecos (3): Desviación típica de Y = Rellenar huecos (4):

Covarianza = Rellenar huecos (5): Coeficiente de correlación r = Rellenar huecos (6):

Según ese valor de r, influye de manera decisiva la cantidad de agua caída, ¿sí o no? Rellenar huecos (7): JXUwMDJiJXUwMDll

Calculamos la recta de regresión X sobre y, pues me pide un valor de X, conocido uno de Y, y sustituimos la y por 250.

recta de regresión: X = Rellenar huecos (8): y + Rellenar huecos (9):

Estimación: Para obtener 250.000 kg de cosecha, deberán caer Rellenar huecos (10): l/m²

Habilitar JavaScript

Importante

La fiabilidad de la estimación de la recta de regresión nos la dará el coeficiente de determinación. Cuanto más cerca esté r² de 0, la fiabilidad de la la predicción será menor, y cuanto más cerca esté de 1 más fiable es la predicción.