4º ESO (Opción B): EVALUACIÓN DEL TEMA DE POLINOMIOS

Escoge la respuesta o las respuestas correctas para cada pregunta, haciendo click sobre la letra o letras correspondientes.

El valor numérico del polinomio 3x⁴ - 2x³ + 3x² - 2x + 1 en el punto x = 2, es:
Si el valor numérico de p(x) en x = 2 es cero, entonces:
1. p(x) es divisible entre x + 2
2. p(2) = 0
3. El resto de la división p(x) : x – 2 es cero.
4. x – 2 es divisor de p(x)
La Regla de Ruffini:
1. Sirve para dividir un polinomio cualquiera entre otro de la forma x – a.
2. Es una forma más cómoda de realizar cualquier división.
3. Es una regla de cálculo de poca utilidad.
Las raíces del polinomio x³ – 7x – 6, son:
1. – 1,– 2 y 3
2. – 1,– 2 y – 3
3. 1,2 y 3
4. 5,2 y 1
El borrón rojo de la siguiente imagen es:
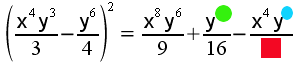
El borrón verde de la siguiente imagen es:
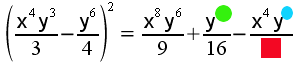
El borrón azul de la siguiente imagen es:
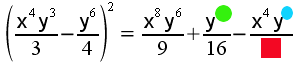
El resultado de calcular (5x – 3)(5x + 3) es:
1. 25x² – 6
2. 25x² – 9
3. 5x² – 9
4. 5x² + 9
El resultado de calcular (3x + 1)² es:
1. 9x² + 1
2. 3x² + 6x + 1
3. 9x² + 6x + 1
4. 9x² + 6x + 2
El valor numérico de p(x) = 2x³ – 3x² + 5x – 1 en x = – 2 es:
El polinomio p(x) = x³ – 2x² – 4x + 12, no podría tener nunca al 5 como raíz porque:
1. Lo dice el Teorema del Resto.
2. La raíz de 5 es irracional.
3. 5 no es divisor de 12.
La descomposición en factores de x³ – 2x² es:
1. x (x² – 2x)
2. x² (x – 2)
3. 2x (x² – 1)
4. 2x (x – 1)
Si al dividir q(x) entre x + a, se obtiene resto cero:
1. q(a) = 0
2. q(– a) = 0
3. x+a es divisor de q(x)
4. q(0) = 0
Las raíces del polinomio 12x³ – 27x son:
1. 3,1.5 y – 1.5
2. 0, 3, 1.5 y – 1.5
3. 0,1.5 y – 1.5
4. No se pueden calcular
El resto de dividir x²⁰ – 11 entre x + 1 es:
1. 10
2. – 12
3. – 10
4. 12
Si el polinomio x¹¹ + 1 es divisible entre x + k, entonces:
1. k = 1
2. k = – 1
3. k = 0
4. k = 2
Si R(x) = (x + 2)( x – 3)x, entonces:
1. R(x) es múltiplo de (x – 3)x
2. R(x) es múltiplo de (x – 3)²x
3. R(x) es múltiplo de (x + 2)²(x – 3)
4. R(x) no tiene múltiplos.
El polinomio 5x²(x + 2)(x – 3) tiene por raíces:
1. 2 y –3
2. –2, 3 y 5
3. 0, –2 y 3
4. 0, 2 y –3
El M.C.D. de los polinomios A(x) = x(x + 2)² y B(x) = 5x²(x + 2)(x – 3) es:
1. 5x(x + 2)²
2. x(x + 2)
3. x²(x + 2)²(x – 3)
4. x²(x + 2)
El m.c.m. de los polinomios A(x) = x(x + 2)² y B(x) = 5x²(x + 2)(x – 3) es:
1. 5x(x+2)²
2. x(x+2)
3. 5x²(x+2)²(x – 3)
4. x²(x+2)
Ejemplos de polinomios de segundo grado con 3 como única raíz son:
1. x²+6x + 9
2. x² – 6x + 9
3. 3x²+18x + 27
4. 2x² – 12x + 18
El resultado de 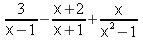es:
El borrón azul de la imagen siguiente en la que se simplifica una fracción algebraica es: $fracciones01.gif$
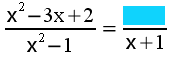
En una división de polinomios :
1. El grado del cociente es igual al grado del dividendo menos el grado del divisor.
2. El grado del resto es un grado menor al grado del divisor.
3. El resto siempre tiene grado cero.
4. La regla de Ruffini siempre simplifica los cálculos.
En una suma de dos polinomios, el grado del polinomio suma:
1. Es igual a la suma de los grados de los sumandos.
2. Es igual a la suma de los coeficientes de mayor grado.
3. Puede ser cero.
4. No puede ser mayor que el mayor de los grados de los sumandos.
Un polinomio de grado 2:
1. Siempre puede descomponerse en factores.
2. Puede no tener raíces reales.
3. Siempre es producto de dos polinomios de grado uno.
4. Tendrá siempre dos raíces distintas.
Un polinomio de grado 3:
1. Como máximo puede tener tres raíces.
2. Puede tener sólo dos raíces.
3. Siempre es producto de tres polinomios de grado 1.