2.1. ¿Por qué uniformemente?... Y más cosas
No es necesario que nos preguntemos por qué rectilíneo o por qué acelerado (variado) ¿Verdad?
Ya sabes que si un movimiento se llama "rectilíneo" es porque su trayectoria es una recta. Y en el apartado anterior has aprendido que, si se llama "acelerado" es porque su velocidad cambia (bueno, en este caso, solo su rapidez, "lo deprisa que va")
Pero, ¿qué significa el "uniformemente"? Observa con atención la imagen...
|
|
| Elaboración propia |
El movimiento de esta bola no es uniforme... ¡ni mucho menos! Observa que no recorre distancias iguales en tiempos iguales.
Por ejemplo, entre los instantes t=0 s y t=1 s solo recorre 1 m, mientras que entre t=2 s y t=3 s recorre 5 m (pasa de la posición e=4 m a la posición e=9 m).
Pero ¿qué sucede con la velocidad de la bola?... En la tabla de abajo lo verás mejor
| Tiempo (s) | Velocidad (m/s) |
| 0 | 0 |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
Cada segundo que pasa la velocidad aumenta en 2 m/s ¿lo ves?
Es decir, la velocidad va cambiando, sí, ¡pero siempre al mismo ritmo!
Por eso la gente de Ciencia llama a este movimiento UNIFORMEMENTE ACELERADO. La velocidad cambia, pero de manera "uniforme"... siempre cambia igual.
Actividad
En un movimiento rectilíneo uniformemente acelerado, la velocidad cambia a un ritmo constante.
Para medir ese ritmo al que varía la velocidad se usa una nueva magnitud: la aceleración.
Caso práctico
¡Es así de fácil!
Veamos... en el ejemplo de antes, cada segundo que pasa la velocidad aumenta en 2 m/s.
¿Cómo se expresa eso?
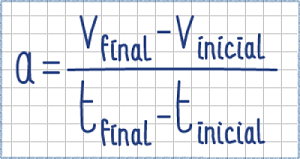
Incluso lo podemos calcular de forma muy facilita. Mira... si la aceleración mide el ritmo al que cambia la velocidad, para calcularla solo tendremos que dividir lo que ha cambiado la velocidad entre el tiempo que ha tardado en cambiar.
| Imagen de elaboración propia |
La unidad de la aceleración en el SI es el "metro por segundo cada segundo". Esa unidad "tan rara" se escribe m/s2 (y se lee "metro por segundo al cuadrado"). Una aceleración de 2 m/s2 significa que cada segundo que pasa el cuerpo se mueve con una velocidad 2 m/s más grande.
Caso práctico
Volviendo al ejemplo…
¿Cuánto ha cambiado la velocidad entre los instantes t=2 s y t=4 s? En el instante t=2 s la velocidad era v=4 m/s y en el instante t=4 s ya era diferente, era v=8 m/s.
Intenta aplicar la fórmula anterior.
Bien... seguro que ya has entendido por qué el movimiento que vas a estudiar se llama uniformemente acelerado, porque su aceleración es constante, no cambia, es siempre la misma (de ahí lo de uniformemente).
Conocimiento previo
¡Ojo con la aceleración!
Debes tener mucho cuidado con esto de la aceleración. Es una palabra que usamos mucho en nuestro lenguaje cotidiano. No es raro escuchar frases como "acelera, acelera... que no llegamos" o "mi hermana está siempre acelerada" o "no aceleres tanto el coche, que lo vas a quemar"... y muchas más por el estilo.
Pero el significado que la palabra "aceleración" tiene en el lenguaje cotidiano no siempre coincide con lo que los científicos entienden por aceleración. Recuerda que... en la ciencia, aceleración significa siempre "cambio de velocidad".
Actividad
|
n |
| Elaboración propia a partir de imágenes en pixabay, autobús y árbol. Dominio público |
Si en el instante inicial →to (tinicial), la velocidad de un cuerpo que se mueve con MRUA es → vo(vfinal); y en un instante posterior →tf(tfinal), la velocidad es →vf(vfinal). Entonces, la aceleración constante del movimiento es:
Caso práctico
Por ejemplo…
 |
| Imagen en flickr de Alex Basnett. Licencia cc |
A.- No todos los fórmula 1 son iguales, claro. Pero no es una barbaridad decir que pueden pasar de cero a cien en unos 2,4 s. Si acelera de manera uniforme, ¿con qué aceleración lo hace?
B.- Claro que, cuando el coche va a toda pastilla... digamos que a 320 km/h y se acerca a una curva que tiene que tomar solo a 80 km/h... no tendrá más remedio que frenar, ¿verdad? Si apura mucho la frenada, supongamos que lo hace en 1,6 s. En ese intervalo de tiempo..., ¿estará acelerando el fórmula 1? ¿Cuál será su aceleración?
¡Nos sale una aceleración negativa! ¿Estará mal hecho el cálculo?
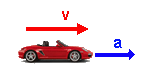
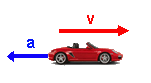
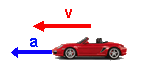
No, no... claro que puede ser una aceleración negativa (igual que una velocidad). La aceleración es también un vector, como la velocidad; importa "hacia dónde" se acelera:
- si se acelera en el mismo sentido en que la velocidad... ésta irá aumentando.
- si se acelera en sentido contrario al que lleva la velocidad... ésta irá disminuyendo (¡vamos frenando!).
Esto no tiene nada que ver con que la aceleración sea positiva o negativa. Eso depende, realmente, del sistema de referencia que hayamos tomado (igual que pasa con la velocidad):
 |
 |
 |
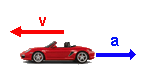 |
| El coche irá cada vez más rápido | El coche irá cada vez más despacio | El coche irá cada vez más rápido | El coche irá cada vez más despacio |
| Elaboración propia | |||