4. Cálculo de áreas de recintos sencillos mediante la integral definida

Por último veamos como calcular áreas encerradas en recintos sencillos:

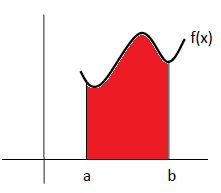Si nos encontramos con un recinto como el de la figura en el que la hay una única función f(x) positiva en todo el intervalo de integración [a, b] para calcular el área del recinto coloreado basta con calcular la integral definida de la función f(x) entre los extremos a y b, es decir basta con calcular:

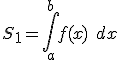
$S_1=\int_a^b f(x) \; dx$

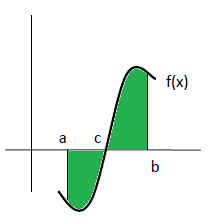Si queremos calcular el recinto que encierra esta segunda gráfica, tenemos que tener en cuenta que la medida de una superficie siempre es positiva, y que en las propiedades de las integrales definidas teníamos que cuando una función es negativa en un intervalo la integral definida en ese intervalo de dicha función es negativa, por lo que si queremos calcular el área del recinto coloreado tendremos que cambiar el signo de la función en el recinto que se encuentra por debajo del eje de abcisas, es decir:

$S_2 =\int_a^c \left[-f(x) \right] \; dx+\int_c^b f(x) \; dx =-\int_a^c f(x) \; dx+\int_c^b f(x) \; dx$

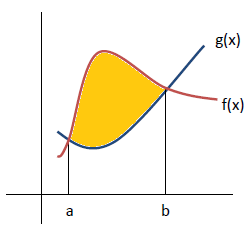Por último, si queremos calcular el área encerrada entre dos funciones como aparecen el dibujo adjunto habría que calcular el área que encierra la función superior y restarle el área que encierra la función inferior en el intervalo de integración que deseemos, o lo que es lo mismo:

$S_3 =S-f - S_g = \int_a^b f(x) \; dx - \int_a^b g(x) \; dx = \int_a^b \left\[ f(x) - g(x) \right\] \; dx$

Reflexión

Determina las áreas de las siguientes figuras coloreadas:


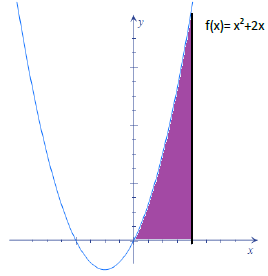Apartado a.	Apartado b.	Apartado c.

Retroalimentación

El área que queremos calcular está encerrada por la función f(x)=x²+2x, el eje de abcisas y la recta x=4. Dicha área se calcula con la integral:

$\int_0^4 \left$x^2+2x \right$ \; dx = \left\[\frac{x^3}{3}+x^2 \right\]_0^4 = \left$\frac{4^3}{3}+4^2 \right$ - \left$\frac{0^3}{3}+0^2 \right$ = \frac{112}{3}$

Este área la calcularemos de dos formas diferentes:

El recinto del que queremos calcular el área consta de dos partes, la primera de ellas se encuentra debajo del eje de abcisas por lo que para calcular el área tenemos que cambiar el signo de la función. Como exponíamos anteriormente, quedando:

$\begin{array}{lcl} S & = & \int_{-\pi}^{0} \left$ - \begin{verbatim}sen\end{verbatim} x \right$ \; dx + \int_{0}^{\pi} \begin{verbatim}sen\end{verbatim} x \; dx = \left\[ \cos x \right\]_{-\pi}^{0} + \left [ -\cos x \right ]_{0}^{\pi} = \\ & = & [\cos 0 - \cos (-\pi) ] + [-\cos \pi -(- \cos (0) ) ] = 2 + 2 = 4 \end{array}$

Este área tambien se podría calcular teniendo en cuenta que la función es simétrica y que el área de la parte de la izquierda es igual que el de la derecha por lo que quedaría:

$\begin{array}{lcl} S & = & 2 \cdot \int_{0}^{\pi} \begin{verbatim}sen\end{verbatim} x \; dx = 2 \cdot \left [ -\cos x \right ]_{0}^{\pi} = \\ & = & 2 \cdot [-\cos \pi -(- \cos (0) ) ] = 2 \cdot [-(-1) -(- 1 ) ] = 2 \cdot 2 = 4 \end{array}$

Para calcular el área que encierra este último recinto, en pirmer lugar hay que determinar los límites de integración. Este proceso resulta sencillo sin más que igualar ambas funciones y calcular los valores de x:

$\begin{array}{lcl} \left\. \begin{array}{lcl} y=2x \\ y=x^2 \end{array} \right\} & \Rightarrow & 2x = x^2 \ \Rightarrow \ x^2- 2x = 0 \ \Rightarrow \ \\ & \Rightarrow & x\cdot (x - 2) = 0 \ \Rightarrow \ \left\{ \begin{array}{c} x=0 \\ \vspace{8}\\ x-2=0 \ \Rightarrow \ x=2 \end{array} \right. \end{array}$

Como podemos apreciar en la figura, la función f(x) está por encima de la función g(x), por lo que el área del recinto quedaría:

$\int_0^2 \left$2x - x^2 \right$ \; dx = \left\[x^2 - \frac{x^3}{3} \right\]_0^2 = \left$2^2 - \frac{2^3}{3} \right$ - \left$0^2 - \frac{0^3}{3} \right$ = \left$4 - \frac{8}{3} \right$ = \frac{4}{3}$

Pregunta de Elección Múltiple

Aquí tienes un listado de actividades con las que puedes practicar el cálculo de áreas y la integral definida. También tienes la opción de ver las soluciones de los ejercicios.

4. Cálculo de áreas de recintos sencillos mediante la integral definida

Reflexión

Retroalimentación

Pregunta de Elección Múltiple

Pregunta

Respuestas

Retroalimentación

Solution

Pregunta

Respuestas

Retroalimentación

Solution

Pregunta

Respuestas

Retroalimentación

Solution