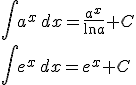1. Primitivas. Cálculo de primitivas inmediatas

Históricamente, la noción de integral es anterior a la de derivada. Esta surge al intentar calcular el área de ciertas figuras.

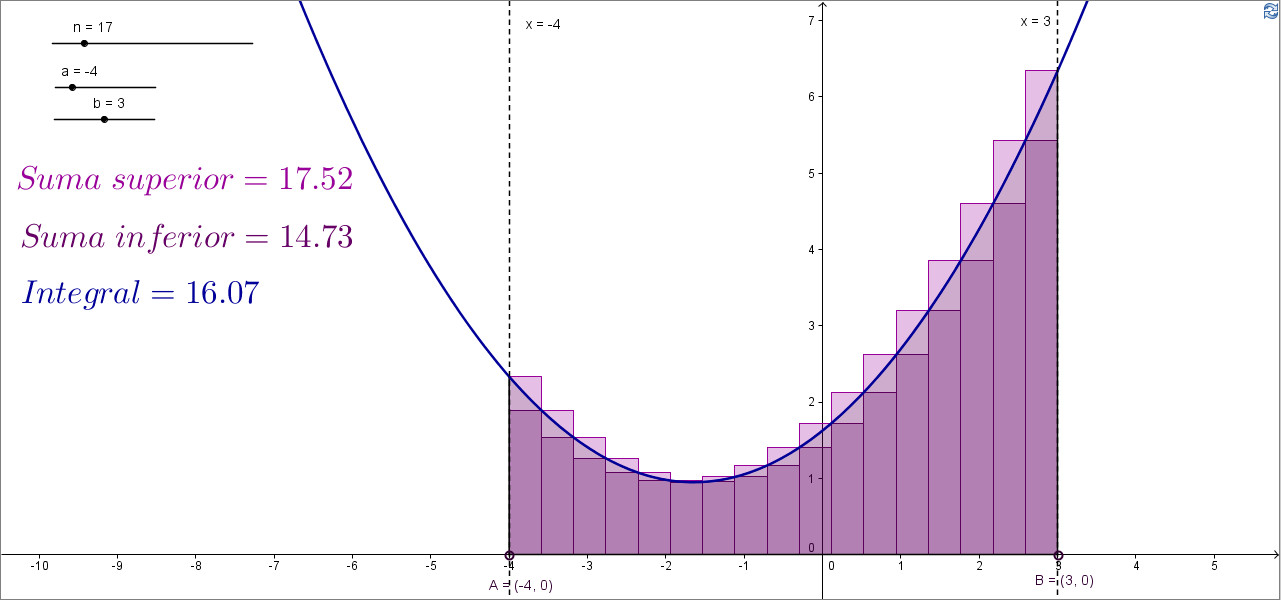
Arquímedes fue el primero que da una cierta aproximación de como calcular el área que se encuentra bajo una cierta curva mediante su método de exhaución, método que consistía, básicamente, en inscribir y circunscribir poligonales en la curva o recinto en cuestión. Estas eran  cada vez más cercanas y calculaba  las áreas de estas poligonales como aproximación de la superficie inicial. Para acercarnos a la idea que expone este método te proponemos el siguiente applets de Geogebra.

El cálculo integral toma un gran impulso con Newton y Leibniz en el siglo XVIII. Estos matemáticos geniales son considerados los padres del cálculo integral.

A pesar de este gran impulso que recibe el cálculo integral no se resuelve totalmente el problema hasta un siglo más tarde con Cauchy y Riemann.


 

A través de la siguiente imagen puedes acceder a una simulación (de matematicafpu bajo CC) en la que ver cómo se utiliza el método de exhaución y cómo se puede aproximar por defecto y por exceso el área delimitada por una función, el eje de abscisas y dos ordenadas a y b.

Actividad

La función F(x) es primitiva de una función f(x) si se cumple que F'(x)=f(x). Teniendo en cuenta esta definición de integral, cualquier función de la forma F(x)+C es también primitiva de f(x).

Al conjunto de todas las primitivas de f(x) se le llama integral indefinida de f(x) y se representa:

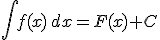\int f(x) \, dx = F(x) +C

Ejemplo

Una rápida lectura de la definición anterior nos lleva a pensar que integrar una función es el proceso inverso de derivar. Al integrar una función obtenemos una nueva F(x)a la que llamaremos primitiva de la anterios y a la que,al derivarla, obtenemos la función de partida. Veamos esto con un ejemplo:

Sabemos que (x3)'=3x2, así pues:

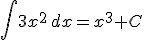
\int 3x^2 \, dx = x^3 +C

donde C es una constante cualquiera.

Establezcamos varias reglas básicas para integrar funciones:

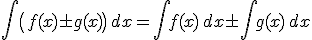
\int \( f(x) \pm g(x) \) \, dx = \int f(x) \, dx \pm \int g(x) \, dx
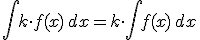
\int k \cdot f(x) \, dx = k \cdot \int f(x) \, dx

donde k simboliza a cualquier número real.

Es decir, que para calcular la integral de la suma o la resta de varias funciones basta con calcular las integrales independientes y sumar sus resultados. Para integrar un número por una función simplemente integraramos la función dada y el resultadolo multiplicamos por el número en cuestión.

Vamos a observar unas integrales inmediatas de funciones simples:

 

Funciones potenciales:

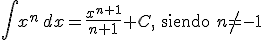
\int x^n \, dx=\frac{x^{n+1}}{n+1}+C,\begin{verbatim}{ siendo }\end{verbatim} n eq -1

Funciones trigonométricas:

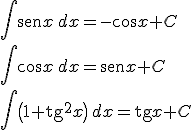
\int\begin{verbatim}sen\end{verbatim} x \, dx = -\cos x + C \\ \int \cos x \, dx = \begin{verbatim}sen\end{verbatim} x + C \\ \int \(1+ \begin{verbatim}tg\end{verbatim}^2 x \) \, dx = \begin{verbatim}tg\end{verbatim} x + C

Funciones inversas de las trigonométricas:

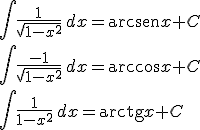
\int \frac{1}{\sqrt{1-x^2}} \, dx = \begin{verbatim}arcsen\end{verbatim} x +C \\ \int \frac{-1}{\sqrt{1-x^2}} \, dx = \begin{verbatim}arccos\end{verbatim} x +C \\ \int \frac{1}{1-x^2} \, dx = \begin{verbatim}arctg\end{verbatim} x +C
Juego de palabras

Imagen en deviantart de cintianightmare bajo CC

Funciones exponenciales:

\int a^x \, dx=\frac{a^x}{\ln a}+C \\ \int e^x \, dx=e^x + C

Funciones logarítmicas:

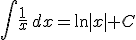
\int \frac{1}{x} \, dx =\ln |x|+C

Pregunta de Elección Múltiple

Pregunta

Calcula las siguientes integrales:

\int \( 3x^2-2x+3- \frac{1}{x} \) \. dx

Respuestas

x^3-\frac{x^2}{2}+3x-\ln |x|+C

\frac{x^3}{3}-x^2+3x-\ln |x|+C

x^3-x^2+3x-\ln |x|+C

Retroalimentación

Pregunta

\int \(3 \cdot \begin{verbatim}sen\end{verbatim} x -\frac{2}{1+x^2} \) \, dx

Respuestas

-3 \cdot \cos x - 2\begin{verbatim} arctg \end{verbatim}x+C

3 \cdot \cos x - 2\begin{verbatim} arctg \end{verbatim}x+C

- 3 \cdot \cos x + 2 \begin{verbatim} arctg \end{verbatim}x+C

Retroalimentación

En la primera hoja de este documento (de José Luis Alejandre Marco y Ana Isabel Allueva Pinilla bajo CC) puedes encontrar actividades resueltas para practicar estos conceptos.