2. Propiedades de la integral definida
 |
|
Imagen de elaboración propia
|
Si tienes en tu casa un robot de cocina, o estás pensando en conseguir uno, seguro que lo primero que te interesó fueron todas las propiedades que tenía dicho aparato. Ver como podía afectar a tus platos tradicionales, qué cosas nuevas podías hacer, como podía simplificarte el trabajo, etc.
Esto mismo ocurre con cualquier herramienta nueva con la que entres en contacto, interesa conocer cuáles son sus propiedades fundamentales y como se aplica a elementos ya conocidos. Eso es lo que vamos a hacer en este apartado con la integral definida.
1) La integral definida de una suma (o resta) de funciones integrables es igual a la suma (o resta) de las integrales definidas de cada función.
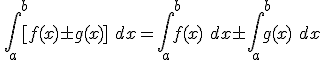
2) La integral definida del producto de una constante por una función es igual al producto de la constante por la integral de la función.
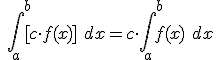
3) Si cambiamos entre sí los límites de integración, el valor de la integral definida cambia de signo.
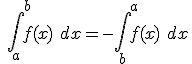
AV - Actividad de Espacios en Blanco
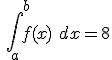 y
y 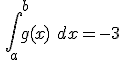 . Se verifica que:
. Se verifica que:
 :
:
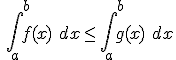
5) Si tenemos un valor c del intervalo [a,b] cualquiera se verifica que:
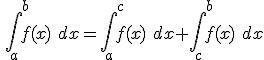
Gracias a la propiedad 3) esta propiedad se puede generalizar a cualquier valor c, independientemente de que esté o no dentro del intervalo [a,b], siempre que las funciones sigan teniendo sentido hasta el valor c.
Podemos ver aplicada esta propiedad en la siguiente ventana.Ejemplo o ejercicio resuelto
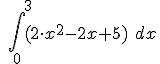 .
.
Ejemplo o ejercicio resuelto
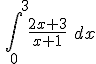
AV - Actividad de Espacios en Blanco
Ejemplo o ejercicio resuelto
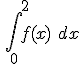 , siendo
, siendo 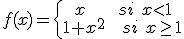 .
.
Ejemplo o ejercicio resuelto
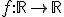 definida en la forma
definida en la forma 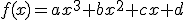 se sabe que tiene un máximo relativo en x=1, un punto de inflexión en (0,0) y que
se sabe que tiene un máximo relativo en x=1, un punto de inflexión en (0,0) y que 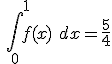 . Calcula a, b, c y d.
. Calcula a, b, c y d.