3.2. Función inversa
Una vez la ropa limpia, seca y planchada, podemos volver atrás en el proceso. Es decir, arrugarla, mojarla y ensuciarla. Parece que sí, que los procesos son reversibles. Con la composición de funciones no siempre es posible, no todas las funciones tienen vuelta atrás. Para ello es necesario que cumplan algunas condiciones.
Por ejemplo, la función 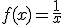 sí es reversible en su dominio. Solo tenemos que pensar qué hace
sí es reversible en su dominio. Solo tenemos que pensar qué hace  con cada número: transformarlo en su inverso. Es decir, la imagen de 2 es
con cada número: transformarlo en su inverso. Es decir, la imagen de 2 es 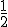 , y la de 5 es
, y la de 5 es 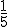 .
.
Piensa un momento, encontrar la función que deshace  , que arruga, moja o ensucia, consiste en hallar la función que convierte
, que arruga, moja o ensucia, consiste en hallar la función que convierte 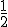 en 2 y
en 2 y 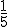 en 5. En general, que a
en 5. En general, que a 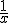 lo convierte en x. Y dicha función es la misma
lo convierte en x. Y dicha función es la misma 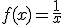 .
.
Como hemos dicho, no todas las funciones son reversibles. Por ejemplo, una función constante 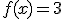 . Todos los puntos
. Todos los puntos 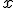 tienen como imagen 3. Si quisiéramos dar la vuelta, ¿cómo lo haríamos? ¿A qué punto iría el 3? ¿Cuál sería el dominio de esta nueva función? ¡Vaya lío!
tienen como imagen 3. Si quisiéramos dar la vuelta, ¿cómo lo haríamos? ¿A qué punto iría el 3? ¿Cuál sería el dominio de esta nueva función? ¡Vaya lío!
Actividad
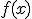 y
y  dos funciones que cumplen que
dos funciones que cumplen que
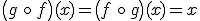
Entonces decimos que  y
y 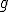 son inversas. A la función
son inversas. A la función 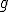 la representaremos como
la representaremos como 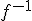 y a la función composición la llamaremos identidad.
y a la función composición la llamaremos identidad.
Gráficamente una función es inversa de otra función cuando sus respectivas gráficas son inversas, es decir, son simétricas respecto de la bisectriz del primer y tercer cuadrante.
Para comprender mejor la relación que existe entre la gráfica de una función y de su inversa, te puedes ayudar de la escena de GeoGebra que aparece al hacer clic en la siguiente imagen.
En ella se puede conseguir la expresión analítica y la gráfica de la inversa de funciones afines. Al tener este tipo de funciones unas gráficas muy sencillas (rectas) se puede apreciar la simetría respecto de la función 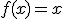 , cuya gráfica es la bisectriz del primer y tercer cuadrante.
, cuya gráfica es la bisectriz del primer y tercer cuadrante.
Practica con la escena e intenta averiguar la expresión y gráfica de la función inversa de varias funciones afines.

|
| Elaboración propia |
Debemos diferenciar entre el inverso de un número y la inversa de una función.
En el primer caso si tenemos un número  , su inverso es
, su inverso es 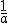 , mientras
que si hablamos de la inversa de una función nos referimos a
, mientras
que si hablamos de la inversa de una función nos referimos a 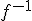 y no a
y no a 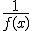 .
.
Ejemplo o ejercicio resuelto
Caso de estudio
Calcula la función inversa de las siguientes funciones:
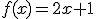 |
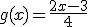 |
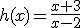 |
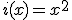 |

