Resumen

Importante

Propiedades de las desigualdades

Sean a, b y c tres números reales.

Si a < b, entonces a + c < b + c para cualquier número c.
Si a < b, entonces a·c < b·c para cualquier número c > 0.
Si a < b, entonces a·c > b·c para cualquier número c < 0.

Las desigualdades no se comportan igual que las igualdades cuando multiplicamos ambos términos por un mismo número.

Estas propiedades pueden enunciarse de la siguiente manera:

- Si a los dos miembros de una desigualdad se le suman o restan un número, la desigualdad no cambia de sentido.

- Si se multiplican o dividen por un número positivo los dos miembros de una desigualdad, entonces esta no cambia de sentido.

- Si se multiplican o dividen por un número negativo los dos miembros de una desigualdad, entonces esta se invierte y cambia de sentido.

Fuente propia realizada bajo Dominio público

Importante

Dados dos números reales cualesquiera, a y b, se pueden dar estas tres relaciones entre ellos:

a < b ; a menor que b. A la expresión la llamamos desigualdad
a = b ; a igual que b. A la expresión la llamamos igualdad
a > b ; a mayor que b. A la expresión la llamamos desigualdad

La segunda relación se denomina igualdad y cuando aparecen letras además de cifras numéricas, reciben el nombre de ecuaciones.

Las relaciones primera y tercera se denominan desigualdades y cuando aparecen letras además de cifras numéricas, reciben el nombre de inecuaciones.

Por otro lado, estas propiedades que cumplen todos los números reales hace que su conjunto, el conjunto de los números reales, sea totalmente ordenado. Hablamos entonces del orden de los números reales.

Otra forma de visualizar las desigualdades y el orden de los números reales sería:

Fuente propia realizada bajo Dominio público

Importante

Resolver una inecuación es encontrar el conjunto de números reales que cumplen la desigualdad. Este conjunto infinito de soluciones será un intervalo de la recta real.

El proceso de resolución consiste en realizar transformaciones (suma, resta, multiplicación o división) de una misma cantidad a ambos miembros de la inecuación hasta llegar a otra en la que la incógnita se encuentre despejada en uno de sus miembros, aparezca un número en el otro y haya un símbolo de desigualdad entre ambos.

El objetivo de estas transformaciones es llegar a obtener uno de los siguientes modelos (donde x es la incógnita y s un número real)

Finalmente, la solución de la inecuación vendrá dada por los infinitos valores que verifican esta última desigualdad, es decir, todos los puntos del intervalo que tienen por extremo inicial (o final) al valor s.

Importante

Los pasos a seguir para resolver sistemas de dos ecuaciones lineales con una incógnita son los siguientes:

Resolvemos cada inecuación por separado.
La solución del sistema es la intersección de las soluciones que hemos obtenido para cada una de las inecuaciones.

Importante

Inecuaciones cuadráticas

Son aquellas que adoptan las siguientes formas:

Siendo a, b y c números reales cualesquiera.

Inecuaciones racionales

Hemos visto, como caso más sencillo, aquellas que adoptan la forma:

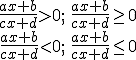Siendo a, b, c y d números reales cualesquiera.