2.4. Racionales
Importante
Inecuaciones racionales
Vamos a ver, como caso más sencillo, aquellas que adoptan la forma:
 |
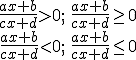siendo a, b, c y d números reales cualesquiera.
Su proceso de resolución es muy parecido al de los sistemas de inecuaciones lineales con una incógnita. Veamos el siguiente ejemplo:
 |
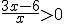Para que la anterior fracción sea mayor que cero se ha de dar alguno de los siguientes casos:
- Numerador y denominador mayores que cero.
En este caso, la resolución de la inecuación equivale a resolver el siguiente sistema de inecuaciones lineales:
 |
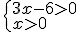Si seguimos los pasos estudiados en el apartado 3 de este tema, obtenemos como solución x > 2.
- Numerador y denominador menores que cero.
En este caso, la resolución de la inecuación equivale a resolver el siguiente sistema de inecuaciones lineales:
 |
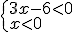Si seguimos los pasos estudiados en el apartado 3 de este tema, obtenemos como solución x < 0.
Conjugando ambas soluciones x > 2 y x < 0, podemos concluir que la solución de la inecuación es: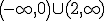 
.
Puede darse el caso de que la inecuación venga expresada de una forma parecida a la siguiente.
 |
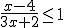Para reducirla a la forma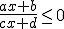 
, vista más arriba, podemos operar sobre la misma mediante las siguientes transformaciones:
 |
 |
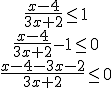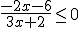Para que la anterior fracción sea menor o igual que cero se ha de dar alguno de los siguientes casos:
- Numerador mayor o igual que cero y denominador menor que cero.
En este caso, la resolución de la inecuación es equivalente a resolver el siguiente sistema:
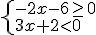
Si seguimos los pasos estudiados en el apartado 3 de este tema, obtenemos como solución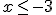 
.
- Numerador menor o igual que cero y denominador mayor que cero.
En este caso, la resolución de la inecuación es equivalente a resolver el siguiente sistema:
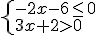
Si seguimos los pasos estudiados en el apartado 3 de este tema, obtenemos como solución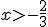 
.
Conjugando ambas soluciones (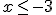 y 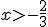) podemos concluir que la solución de nuestra inecuación es: 
.
Comprueba lo aprendido
Ejercicio Resuelto
Halla todos los valores de x para los que 
.