4.2. Exponencial

Albert A. Barlett (1923) eminente profesor de Física de la Universidad de Colorado aseguró en cierta ocasión:

"El mayor defecto de la raza humana es nuestra incapacidad para comprender la función exponencial"

 

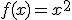Ya hemos estudiado las funciones cuadráticas, en particular la más sencilla de todas ellas: . ¿Qué ocurre si cambiamos los papeles y la base es una constante y el exponente una variable? Obtendríamos una función 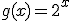, llamada función exponencial.

Actividad

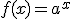Las funciones del tipo ; donde es un número real positivo (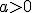) y distinto de 1, se llaman funciones exponenciales.

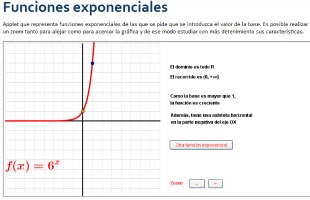
Para conocer todas las características de las funciones exponenciales, puedes hacer clic en la imagen siguiente y acceder al  apartado correspondiente del proyecto EDAD.

Proyecto EDAD

AV - Actividad de Espacios en Blanco

Vamos a comparar la función cuadrática anterior f(x), con la función exponencial g(x). Rellena los espacios en blanco, con estos valores que le asociamos a la variable independiente x:
x f(x)=x2
g(x)=2x
0
1
-1
2
10

Habilitar JavaScript

AV - Actividad de Espacios en Blanco

Si haces clic en la siguiente imagen, puedes acceder a una escena de GeoGebra creada por Jesús Fernández. Con ella es posible representar la gráfica de funciones exponenciales del tipo 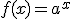. Utilízala para completar los siguientes espacios en blanco, donde se expresan algunas propiedades de este tipo de funciones.

 

Escena de GeoGebra

 

  1. Para que sea una función exponencial a no puede ser ni menor que .

  2. El dominio de la función exponencial no depende de y es

  3. La imagen de 0 siempre vale

  4. La función es creciente si a es mayor que

  5. La función es decreciente si a es menor que

  6. f tiene una asíntota horizontal en .

Habilitar JavaScript

Ejemplo o ejercicio resuelto

Microscopio
Fotografía en Flickr por kasi metcalfe bajo CC

Algunas bacterias se reproducen por mitosis, es decir, se dividen en dos cada pequeño intervalo de tiempo, dejando la misma carga de ADN en ambas partes. Vamos a imaginar que trabajamos en un laboratorio y estamos estudiando este tipo de bacterias. No es que la vida de millones de personas dependa de nosotros, pero formamos parte de un proyecto secreto...

Si estas bacterias se dividen cada 15 minutos y al principio del día sólo hay una, ¿cuántas habrá al final del día?


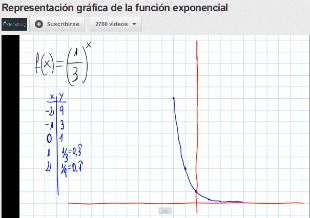
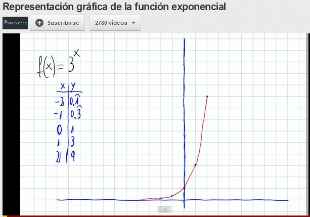
Si haces clic en las siguientes imágenes puedes acceder a dos vídeos donde juanmemol explica los pasos que hay que dar para representar funciones exponenciales con lápiz y papel. En una de ellas la base de la función exponencial es menor que uno y en la otra mayor.

   

Actividad

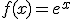Una función exponencial muy utilizada es , siendo 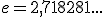Estas funciones aparecen con mucha frecuencia en problemas económicos, biológicos, químicos...

En un apartado anterior ya hemos hablado de la suma de funciones, si una de las funciones es una constante, el efecto que se produce al sumarla a otra función es un desplazamiento o traslación de su gráfica.

En las dos imágenes siguientes se puede apreciar cómo se ha desplazado la gráfica de la función 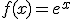al restarle la función constante .

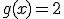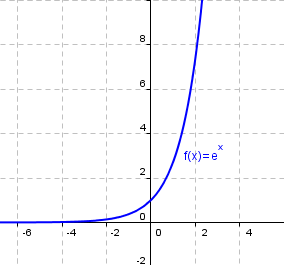Gráfica de la exponencial
Gráfica de la exponencial desplazada
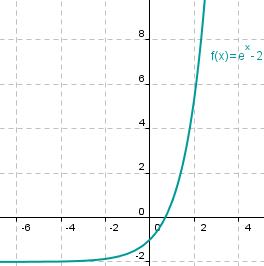Imágenes de elaboración propia

AV - Actividad de Espacios en Blanco

En las siguientes tablas, vamos a recoger algunos valores de las siguientes funciones exponenciales: y=5x, y=5x+3, y=5x-2, y=5x+3, y=5x-2.

x y=5x
y=5x +3
 y=5x -2
-2
-1
0
1
2

x y=5x y=5x+3 y=5x-2
-2
-1
0
1
2

Al representar las funciones y=5x+3 e y=5x-2 se observa que son traslaciones de la gráfica y=5x.

Al representar las funciones y=5x+3 e y=5x-2 se observa que son traslaciones de la gráfica y=5x.

Habilitar JavaScript