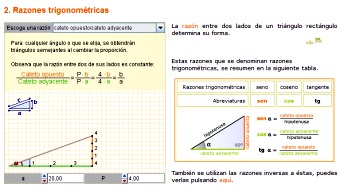
4.1. Trigonométricas
Mira con detenimiento y asombro el siguiente vídeo.
No creas que es un viento huracanado el que produce la ondulación de la plataforma del puente. Son ráfagas de 65 km/h. El fenómeno se conoce como resonancia. La curva que describe tiene un nombre, una sinusoide, y existe una familia de funciones con las que se puede representar y estudiar, las funciones trigonométricas.
Como su propio nombre indica, en la definición de esta familia de funciones intervienen las razones trigonométricas de un ángulo. Nosotros centraremos nuestra atención en las funciones que derivan del seno, coseno y tangente. Para saber más sobre ellas puedes hacer clic en la siguiente imagen, el enlace te llevará a una página del proyecto EDAD.
Actividad
- La función seno es aquella que a un número real
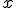 le asocia el seno de ese número, es decir
le asocia el seno de ese número, es decir 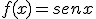 .
. - La función coseno la que a un número real
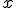 le asocia el coseno de ese número, es decir
le asocia el coseno de ese número, es decir 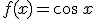 .
. - Por último, la tangente la que a un número real
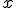 le asocia la tangente de ese número, es decir
le asocia la tangente de ese número, es decir 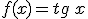 .
.
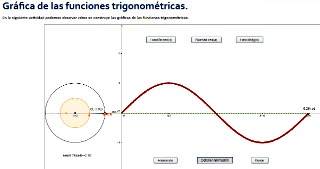
Haciendo clic sobre la siguiente imagen, puedes acceder a una escena de GeoGebra creada por vivianalloret1, en la que se dibuja el trozo de gráfica correspondiente al intervalo [ 0, 2Π] de las tres funciones anteriores.
Para todas ellas la gráfica se repite tanto a la izquierda como a la derecha de dicho intervalo, es decir, la gráfica es idéntica en los intervalos 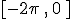 ó
ó 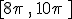 , por ejemplo.
, por ejemplo.
A las funciones con esta característica, que se repiten cada cierto intervalo, se denominan periódicas, y se llama periodo a la longitud del citado intervalo.
Recordamos que la tangente de un ángulo se podía definir como el cociente entre el seno y el coseno de ese ángulo. Por tanto, antes de estudiar la función tangente nos detendremos en las funciones seno y coseno.
Actividad de Espacios en Blanco
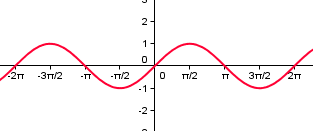 |
| f(x)=sen (x) |
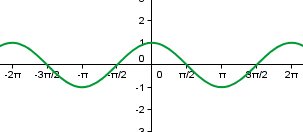 |
| g(x)=cos (x) |
Y completa sus propiedades con los siguientes términos: coseno, seno, decreciente, creciente, periódicas, -1, R, 1.
AV - Pregunta de Elección Múltiple
Solución
- El dominio de esta función son los números reales excepto los múltiplos de ∏/2.
- Su recorrido, todos los números reales.
- Es periódica de periodo ∏.
- Es creciente en todo su dominio.
- Tiene una simetría impar.
Desde el punto de vista matemático las gráficas de las funciones seno y coseno son formas perfectas, paradigmáticas, de bellas y armoniosas ondas. A partir de ellas se construyen los demás movimientos “armónicos”. Destacan por su periodicidad y repetición cíclica.
Muchos fenómenos que se observan en la naturaleza son periódicos y revisten carácter cíclico. La vida está medida y gobernada por la sucesión de días y noches, veranos, inviernos, años... El cuerpo humano está constantemente animado por ritmos fisiológicos, latidos, respiraciones... Las máquinas que el hombre inventa están gobernadas por la repetición a intervalos regulares de tiempo, incluso la actividad social, como la música, o las elecciones democráticas tienen también su ritmo cíclico.
 |
 |
| Fotografía en Flickr por wanderingnome bajo CC |
Fotografía en Flickr por shindoverse bajo CC |
Caso de estudio
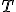 , en grados centígrados, en una cierta ciudad, en un día de primavera, viene dada por la función:
, en grados centígrados, en una cierta ciudad, en un día de primavera, viene dada por la función: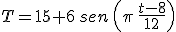
donde 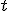 es el tiempo medido en horas desde la medianoche.
es el tiempo medido en horas desde la medianoche.
- ¿Cuál es la temperatura a las 8 h, a las 12 h y a las 6 de la tarde?
- Representa gráficamente la función.