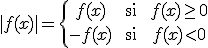3.3. Funciones definidas a trozos
Recuerdas el vídeo del electrocardiograma que aparecía en la introducción de este apartado. La gráfica que describen los impulsos eléctricos del corazón es muy reconocible y algo complicada de clasificar. Podríamos decir que está formada por "remiendos" de funciones lineales que se unen trozo a trozo.
En la siguiente escena de GeoGebra creada por Jesús Fernández, se simula un electrocardiograma que está compuesto por cinco funciones lineales, cada una de ellas definida en un intervalo de números reales.
Caso de estudio
Observa la gráfica de más abajo. Es un caso particular generado por la escena de GeoGebra anterior.
Escribe los intervalos en que está dividida la función que tiene como gráfica ese "electro". Halla también la expresión analítica de cada uno de los intervalos.
 |
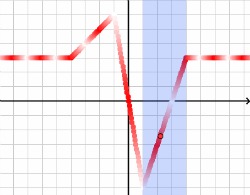| Imagen de elaboración propia |
Importante
Una función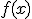 
se dice una función definida a trozos si no está definida
mediante una única expresión en todo su dominio, de tal manera que dependiendo del trozo o intervalo que se considere estará definida de una forma diferente.
El dominio de una función definida a trozos es la unión de cada uno de los intervalos en los que está dividida, si bien hay que tener en cuenta los valores en los que no esté definida la expresión correspondiente.
Generalmente una función definida a trozos se expresa de la siguiente forma:
Caso de estudio
Los intervalos en que está definida una función a trozos pueden ser abiertos, cerrados o abiertos en un extremo y cerrados en el otro. Aunque esto pueda parecer una cuestión sin importancia, la tiene en los casos en que el punto extremo no pertenezca a ninguno de los dos intervalos que separa o bien, no coincidan las imágenes en el punto de las funciones definidas en dichos intervalos correlativos.
Si haces clic en el punto 11 de este enlace puedes acceder a una página de Vitutor donde se representan tres funciones definidas a trozos, y puedes ver con claridad cómo afecta el que un punto extremo pertenezca o no a los intervalos que separa.
Caso de estudio
 |
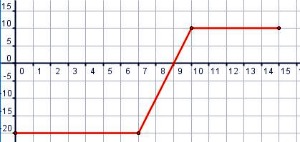| Imagen de elaboración propia |
Lola, a las siete de la mañana, cuando se despierta, saca del congelador la comida que calentará al mediodía cuando vuelva de trabajar. En la gráfica que aparece a la derecha se puede ver cómo va cambiando la temperatura del alimento desde medianoche hasta las tres de la tarde, que es cuando llega Lola del trabajo.
Halla la expresión analítica de la función a trozos que define esa gráfica.
Actividad de rellenar huecos
Completa los espacios en blanco sobre la siguiente gráfica de una función a trozos:
 |
| Imagen de elaboración propia |
Recuerda que en el conjunto de los números reales teníamos una operación llamada valor absoluto. Esta operación no afecta a los números positivos, mientras que a los negativos les cambia el signo.
Esto nos permite definir una función, valor absoluto, que tiene un
efecto parecido: si el valor de 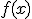es positivo, lo deja igual, en
tanto que si 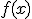es negativo, lo cambia de signo.
Importante
Si tenemos una función real 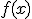, podemos definir la función valor absoluto de 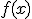como:
