1.1. Definición y formas de expresión
Relacionar dos variables, ese parece ser el objetivo fundamental de las funciones. Pero, ¿cómo es posible llevar a cabo ese fin? ¿Qué herramientas utilizan las matemáticas para realizarlo?
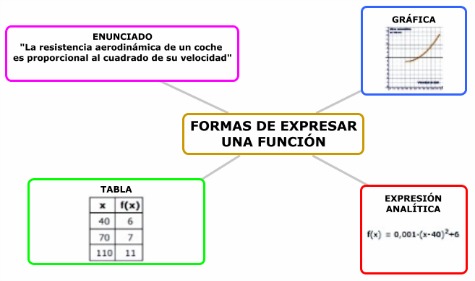
Como veremos a continuación, una relación funcional se puede expresar mediante una gráfica, una tabla o una fórmula. Pero también es posible hacerlo con un enunciado.
Lee con atención el artículo publicado en el blog del diario El País, ecolab, dedicado a cuestiones medioambientales.
| Haz clic en la imagen para ampliar |
Todo el artículo es muy interesante, pero nos vamos a fijar en los siguientes párrafos:
"La resistencia aerodinámica de un coche es proporcional al cuadrado de su velocidad. Esto significa que, efectivamente, el consumo de un carburante será muy alto a 120 kilómetros por hora y descenderá de forma considerable si se levanta el pie del acelerador".
"(...) cuando la aguja del velocímetro pasa a velocidades muy bajas (por debajo de 40 km/h), el consumo por kilómetro puede volver a subir".
¿Qué dos variables se relacionan en ese artículo? ¿Es una relación funcional, es decir, una función? En ese caso, ¿cómo se relacionan dichas variables? ¿Cómo se representa gráficamente? ¿Qué quiere decir eso de que la resistencia es proporcional al cuadrado de la velocidad? ¿Habrá una fórmula para expresar esa función?
Importante
Se define función real de variable real, como una relación que asocia a un número 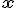 de un conjunto inicial (subconjunto de los números reales), otro número
de un conjunto inicial (subconjunto de los números reales), otro número 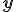 de un conjunto final (números reales). El número
de un conjunto final (números reales). El número 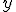 es único, es decir, a
es único, es decir, a 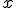 no se le puede asociar más de un número.
no se le puede asociar más de un número.
A las funciones se les suele llamar 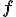 , y la relación se expresa de la siguiente manera:
, y la relación se expresa de la siguiente manera: 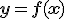 .
.
La variable 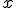 , la que es objeto de estudio de la función, recibe el nombre de variable independiente. En tanto que la variable
, la que es objeto de estudio de la función, recibe el nombre de variable independiente. En tanto que la variable 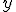 , dado que sus valores dependen de
, dado que sus valores dependen de 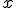 , se denomina variable dependiente.
, se denomina variable dependiente.
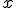 ="velocidad del vehículo", e
="velocidad del vehículo", e 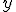 ="consumo de carburante". A cada velocidad, variable independiente, le corresponde un único consumo, variable dependiente.
="consumo de carburante". A cada velocidad, variable independiente, le corresponde un único consumo, variable dependiente.
Ejemplo o ejercicio resuelto
El 11 de agosto de 2010, en la ciudad costera de Isla Cristina, en Huelva, las mareas altas fueron a las 4:41 y 16:59 horas. En tanto que las mareas bajas tuvieron lugar a las 10:42 y 23:14 horas.
En la siguiente imagen, obtenida de la página Tabla de mareas, podemos ver cómo variaron las mareas el citado 11 de agosto en Isla Cristina.
 |
| Imagen de elaboración propia |
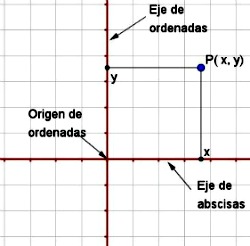
Como puedes apreciar en el ejercicio anterior, una forma de expresar una función es mediante una gráfica. En matemáticas la herramienta que se emplea para representar objetos matemáticos en dos dimensiones es el plano cartesiano.
Este plano cartesiano está formado por dos rectas graduadas numéricamente y perpendiculares entre sí. Al eje horizontal se le denomina de abscisas o eje X, en tanto que al vertical se le llama de ordenadas o eje Y. El origen de ordenadas, que se denomina O, es el punto donde se cortan los dos ejes.
Las escalas en la que se miden ambos ejes pueden no coincidir. Cualquier punto del plano cartesiano viene determinado por dos coordenadas, la abscisa 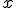 , y la ordenada
, y la ordenada 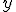 .
.
Si quieres practicar un poco con la representación de puntos en el plano cartesiano, puedes utilizar la siguiente página de Genmagic.
A la hora de representar una función, la variable independiente toma valores en el eje de abscisas y la dependiente en el de ordenadas.
La gráfica de la función estará formada por los puntos 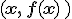 .
.
Por ejemplo, el punto 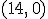 pertenece a la gráfica de la variación de las mareas en Isla Cristina, porque a las 14 horas la altura de la marea es 0 metros, es decir
pertenece a la gráfica de la variación de las mareas en Isla Cristina, porque a las 14 horas la altura de la marea es 0 metros, es decir 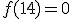 . Pero el punto
. Pero el punto 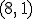 no pertenece a esa gráfica, ya que a las 8 horas la altura de la marea no era de 1 metro, o lo que es lo mismo
no pertenece a esa gráfica, ya que a las 8 horas la altura de la marea no era de 1 metro, o lo que es lo mismo 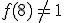 .
.
AV - Actividad de Espacios en Blanco
Otra forma de expresar una función es mediante una tabla de dos columnas. En la primera se irán escribiendo algunos valores de la variable independiente 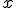 , y en la segunda los valores correspondientes de la variable dependiente
, y en la segunda los valores correspondientes de la variable dependiente 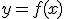 .
.
 |
| Imagen de elaboración propia |
Por ejemplo, en el caso de la gráfica anterior, nos quedaría la siguiente tabla.
| x |
f(x) |
| 40 | 6 |
| 70 | 7 |
| 110 | 11 |
Por último, una función también se puede expresar mediante una fórmula o expresión analítica que relacione las dos variables. Para saber los valores asociados a la variable independiente, basta con sustituirlos en dicha fórmula y operar.
En el caso de los litros consumidos en función de la velocidad, la expresión analítica que los relaciona es 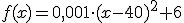 . Por ejemplo, y como ya vimos en la tabla anterior, para saber los litros consumidos si vamos a 40 km/h, basta con sustituir en la fórmula
. Por ejemplo, y como ya vimos en la tabla anterior, para saber los litros consumidos si vamos a 40 km/h, basta con sustituir en la fórmula
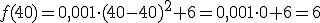
Ahora sí podremos saber con exactitud los litros que corresponden a cada velocidad.
