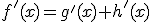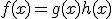2.3. Álgebra de derivadas
Importante
Las principales reglas del álgebra de derivadas son las dos que te proponemos seguidamente. Si tenemos dos funciones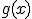 
y 
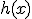, la derivada de la suma y el producto de ambas se obtiene de la siguiente forma:
|
Derivada de una suma. Mariano Real
Vídeo alojado en Youtube
|
Derivada del producto y de la potencia. Mariano Real
Vídeo alojado en Youtube
|
|
Derivada de la suma de funciones
|
Derivada del producto de funciones
f'(x)=g'(x)h(x)+h'(x)g(x) |
AV - Reflexión
Dadas las funciones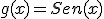 
y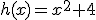 
Calcula la derivada de la suma y el producto de ambas.
Importante
Normalmente, las funciones que solemos encontrarnos no son funciones simples como las que vemos en la tabla de derivadas, sino que son funciones que se obtienen como composición de funciones simples.
Por ejemplo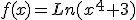 
, en este caso vamos a aplicar lo que se conoce con el nombre de regla de la cadena.
Si llamamos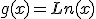 
y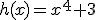 
tenemos que 
.
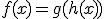la regla de la cadena nos dice que
En nuestro caso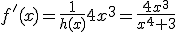 
Ejemplo o ejercicio resuelto
Aplica la regla de la cadena para obtener la función derivada de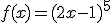 
Una aplicación de la regla de la cadena para las funciones trigonométricas la observamos en el siguiente vídeo:
AV - Reflexión
En el siguiente enlace vas a poder corregir tus prácticas ralizadas. Prueba con cualquier función, e introdúcela. Recuerda que para la función seno deberás introducir sin(x); para logaritmo neperiano log(x) y para cualquier otra base: log_7(x).
AV - Reflexión
Ahora te toca practicar a tí. Para ello te proponemos que calcules la derivada de cada una de las siguientes funciones:
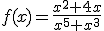
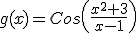
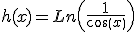
Ejemplo o ejercicio resuelto
Si ahora tenemos una función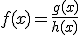 
te proponemos que, aplicando todo lo anterior, calcules su derivada.
Para saber más
Ahora te toca practicar todo lo que puedas los contenidos de la unidad. Para seguir profundizando en la práctica con derivadas te facilitamos este documento:
También puedes observar la siguiente calculadora de derivadas que las realiza paso a paso utilizando la regla de la cadena.