2.2. Función derivada. Reglas de derivación
Importante
Si tenemos una función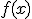 
denominamos función derivada de 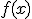respecto a la variable 
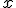a una nueva función que para cada valor 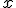nos proporciona la derivada de la función en el punto 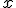. A la función derivada de 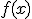la denotaremos 
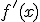, aunque también la puedes ver representada como 
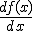. De esta forma tenemos que:
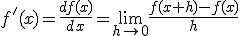
Recuerda que con esta definición, la función derivada nos proporciona, para cada punto 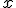, la pendiente de la recta tangente a la función en en punto .
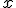Ejemplo o ejercicio resuelto
 |
| Carretera Imagen obtenida del banco de imágenes del ITE |
En la construcción de una carretera, uno de los puntos con los que hay que tener especial cuidado es en las curvas. Dependiendo de lo cerrada que sea la curva, debe tener más peralte o menos para evitar que los coches se salgan de la misma. En la construcción de una carretera, una de las curvas se adapta perfectamente a la función 
. Los técnicos desean tener una función que les proporcione en cada uno de los puntos de la curva la pendiente que tendrá la recta tangente a la misma. ¿Puedes ayudarles?
Por lo general a la hora de derivar un función no aplicamos la definición de derivada tal como hemos hecho en el ejercicio resuelto anterior, sino una serie de reglas de derivación predeterminadas. En la siguiente imagen te ofrecemos un listado de las mismas, en ella se muestra una serie de funciones con su derivada al lado. Este mismo listado te lo ofrecemos en el siguiente documento. Como has podido observar, todos los resultados que aparecen en esta tabla son fruto de aplicar la definición de derivada de una función. Es conveniente aprenderse esta tabla para no tener que recurrir una y otra vez a la definición cada vez que necesitemos derivar una función.
AV - Reflexión
Calcula la derivada de las siguientes funciones:
a)  |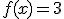
b)  |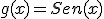
c)  |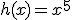
d)  |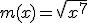
En la siguiente escena puedes introducir en la ventana inferior (donde pone: Entrada...) La expresión de cualquier función (por ejemplo: f(x)=x^5+1) y obtener la expresión de su derivada. A continuación te dejamos el enlace a un manual sobre la introducción de funciones en Geogebra.
También puedes utilizar la siguiente calculadora de WolframAlpha para hallar derivadas.