Resumen

Las funciones del tipo f(x)=a^x; donde a es un número real positivo (a>0) y distinto de 1, se llaman funciones exponenciales.

Una función exponencial muy utilizada es f(x)=e^x, siendo e= 2,718281... Estas funciones aparecen con mucha frecuencia en problemas económicos, biológicos, químicos...

Las funciones logarítmicas son funciones del tipo f(x)= log_ax, donde a es un número real postivo (a>0) y distinto de 1 (a≠1)

• La función seno es aquella función que a un número real x, le asocia el seno de ese número, es decir f(x)=sen x.
• La función coseno es aquella función que a un número real x, le asocia el coseno de ese número, es decir f(x)=cos x.
• La función tangente es aquella función que a un número real x, le asocia la tangente de ese número, es decir f(x)=tg x.

Si en la gráfica de una función observamos que los valores se repiten siempre cada cierto intervalo, decimos que la función es periódica, y a la longitud de este intervalo se le llama periodo. Es decir, si T es el periodo f(x)=f(x+T).

Dadas dos funciones, f y g, se llama función compuesta de f con g a la función

que cumple que:

Sean f(x) y g(x) dos funciones que cumplen que

Entonces decimos que f y g son inversas. A la función g la representaremos como f^-1 y a la función composición la llamaremos identidad.

Gráficamente una función es inversa de otra función cuando sus respectivas gráficas son inversas, es decir, son simétricas respecto de la bisectriz del primer y tercer cuadrante.

Las inversas de las funciones trigonométricas , se nombran como arcsen(x), arccos(x) y arctg(x) :

f(x)=arcsen(x)	f(X)=arccos(x)
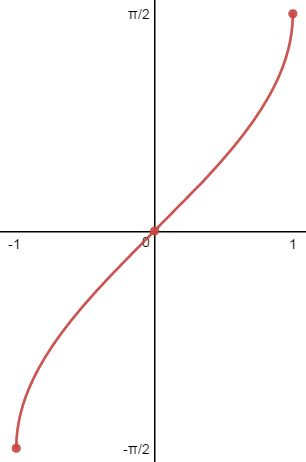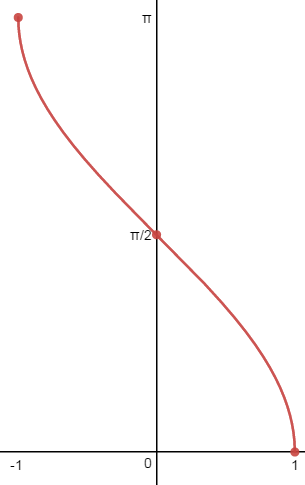Dominio:[-1,1] Recorrido:	Dominio:[-1,1] Recorrido:

f(x)= arctg

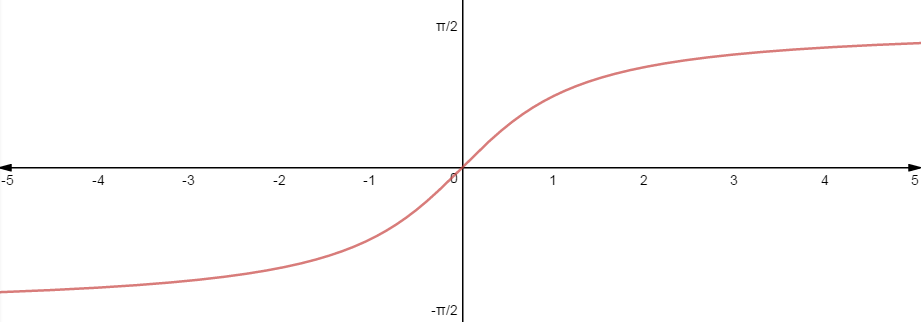Dominio: Recorrido:

Es decir, si queremos calcular arccos(x), estaríamos buscando un ángulo cuyo coseno fuera x:

arccos(x)= cos()=x