6. Función inversa
 |
| Imagen de Jasoon en Flickr. Licencia CC by 2.0 |
¡Ya está bien de experimentar! Pero antes de colgar el cartel de cerrado al laboratorio, quizás deberíamos devolver las cosas a su forma primitiva. Si la base de todos nuestros experimentos era la variable independiente x, ¿sería posible después de tantas composiciones volverla a su "identidad"?
Para ello debemos hacer una última mezcla...
Importante
Sean f(x) y g(x) dos funciones que cumplen que
Entonces decimos que f y g son inversas. A la función g la representaremos como f-1 y a la función composición la llamaremos identidad.
Gráficamente una función es inversa de otra función cuando sus respectivas gráficas son inversas, es decir, son simétricas respecto de la bisectriz del primer y tercer cuadrante.
Observemos la siguiente escena de Geogebra, en ella aparecen dos funciones muy conocidas f(x)=ex y g(x)=ln(x). Otra forma de averiguar que dos funciones son inversas es comprobando que si el punto (a,b) pertenece a la gráfica de la primera función, entonces (b,a) pertenecerá a la gráfica de la segunda.
Ejercicio Resuelto
Calcula la función inversa de f(x)=3x+2
Reflexiona
¿Recuerdas el ejercicio resuelto de las bacterias que se reproducían por mitosis? Sí, aquellas que se dividían cada 15 minutos. En aquel ejercicio vimos que, el número de bacterias que había, pasado un tiempo, se podía expresar mediante la función f(x)=2x, donde x representaba los cuartos de hora que habían transcurrido desde el principio del día.
Nos preguntamos, ¿cuántos cuartos de hora habrán pasado si el número de bacterias que hay es 32768? ¿Y en el caso de que hayan y bacterias, cuántos cuartos de hora habrán transcurrido? Por último, ¿cuál es la función inversa de f(x)?
Una vez que ya conoces el concepto de función inversa, nos vamos a detener en tres funciones especialmente importantes, que resultan ser las inversas de las funciones trigonométricas que hemos visto en apartados anteriores. Así, las funciones senx, cosx y tg x, tendrán sus funciones inversas, siempre y cuando tomemos el dominio adecuado para asegurarnos de que a cada valor de su dominio la función le asocia un único valor del recorrido.
Importante
Las inversas de las funciones trigonométricas , se nombran como arcsen(x), arccos(x) y arctg(x) :
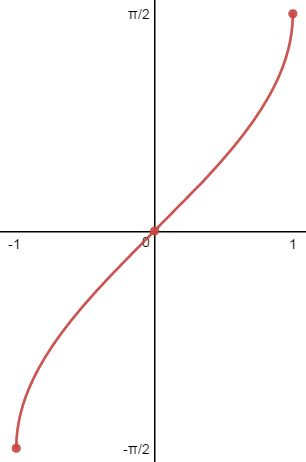
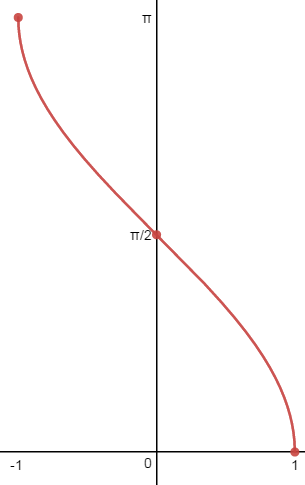
| f(x)=arcsen(x) | f(X)=arccos(x) |
 |
 |
|
Dominio:[-1,1] Recorrido: |
Dominio:[-1,1] Recorrido: |
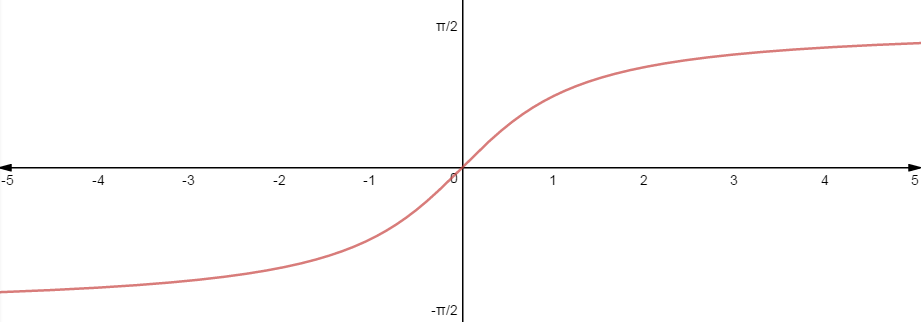
| f(x)= arctg |
 |
|
Dominio: Recorrido: |
Es decir, si queremos calcular arccos(x), estaríamos buscando un ángulo cuyo coseno fuera x:
arccos(x)= ![]()
![]() cos(
cos(![]() )=x
)=x
Curiosidad
Debemos diferenciar entre el inverso de un número y la inversa de una función.
En el primer caso si tenemos un número a, su inverso es 1/a, mientras que si hablamos de la inversa de una función nos referimos a f-1, no a 1/f(x).