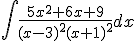2.1. Integración de funciones racionales
En el caso de tener que realizar una integral de la forma
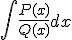donde 
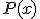y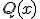 
son funciones polinómicas. En este caso, vamos a intentar descomponer el anterior cociente de funciones polinómicas en fracciones más sencillas.
Si el grado del polinomio 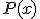es mayor que el grado del polinomio 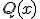, podemos hacer la división efectiva y tendremos que
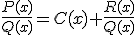donde 
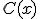y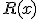 
son funciones polinómicas, cumpliéndose que el grado de 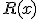es menor que el de 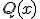. Así, tenemos que
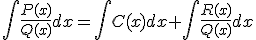
En el siguiente PDF encontrarás información de cómo debemos abordar este tipo de integrales:
Ejemplo o ejercicio resuelto
Calcula la siguiente integral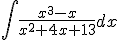 
En la siguiente ventana interactiva te ofrecemos distintas resoluciones que van a poder tener integrales de este tipo, dependiendo de la forma que tengan. Pulsa sobre esta ventana para ir observando la explicación poco a poco y observa los ejemplos que se recogen.
Ejemplo o ejercicio resuelto
Dada la siguiente función 
represéntala gráficamente en la siguiente ventana, sabiendo que la constante que resulta de la integral es 1.
Ejemplo o ejercicio resuelto
Representa gráficamente la siguiente función en la ventana interactiva anterior:
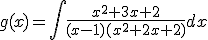
Sabiendo que la constante es 0.
AV - Reflexión
Calcula las siguientes integrales:
a)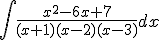 
b)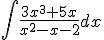 
c) 