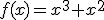1.1. Primitiva de una función
Comenzamos esta parte recordando un poco las derivadas. Para ello, más abajo, hemos incluido una ventana interactiva con la que puedes recordar las derivadas de las funciones más comunes. Además, debes tener en cuenta que si tenemos una función 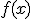 , su derivada es
, su derivada es 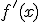 , pero si tenemos otra función
, pero si tenemos otra función 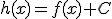 , siendo
, siendo 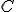 un número cualquiera, su derivada es
un número cualquiera, su derivada es 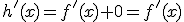 .
.
Así, la derivada de una función va a ser la misma si a esa función le sumamos un número cualquiera.
La pregunta que nos hacemos ahora es: si conocemos la función derivada de otra, ¿podemos conocer la función de la que es derivada?. En algunos casos es bastante sencillo de resolver. Por ejemplo, si tenemos la función 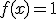 y sabemos que esta función es derivada de otra, la función de la que es derivada es
y sabemos que esta función es derivada de otra, la función de la que es derivada es 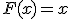 . Ya que sabemos que
. Ya que sabemos que
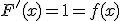
Pero teniendo en cuenta lo que hemos indicado más arriba, 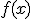 también es la función derivada de la función
también es la función derivada de la función 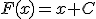 , siendo
, siendo 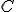 un número cualquiera.
un número cualquiera.
Importante
Si tenemos una función 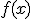 llamamos primitiva de
llamamos primitiva de 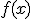 respecto a la variable
respecto a la variable 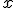 a la función
a la función 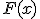 que cumple que:
que cumple que:
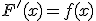
Tal como hemos visto, si 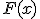 es una primitiva de la función
es una primitiva de la función 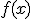 , también lo es
, también lo es 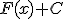 , siendo C un número cualquiera. Por eso llamamos integral indefinida de f(x) al conjunto de todas las primitivas de dicha función. Se representa de la siguiente forma:
, siendo C un número cualquiera. Por eso llamamos integral indefinida de f(x) al conjunto de todas las primitivas de dicha función. Se representa de la siguiente forma:
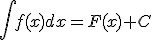
Al símbolo 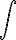 se le llama integral, a la función f(x) integrando y dx es la diferencial y nos indica respecto a qué variable se está hallando la integral.
se le llama integral, a la función f(x) integrando y dx es la diferencial y nos indica respecto a qué variable se está hallando la integral.
Tal como hemos visto anteriormente, si tenemos la función 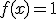 sabemos que:
sabemos que:
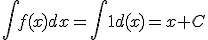
Ya sabemos que la integración es el proceso inverso de la diferenciación o derivada. Por este motivo, conociendo las propiedades de las derivadas y la tabla de derivadas de las funciones, conocemos también la función integral de funciones específicas. Así, algunas de la integrales que conocemos directamente las podemos observar en el siguiente PDF:
Ejemplo o ejercicio resuelto
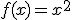
AV - Reflexión
Calcula la integral de la función
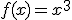
AV - Reflexión
Calcula la integral de la función