4.3. Concavidad, convexidad y puntos de inflexión

Cóncavo
 Cóncavo (abajo) y convexo (arriba)
 		Convexo
Cóncavo Cóncavo (abajo) y convexo (arriba) Convexo
Fotografía en Flick de Tutty bajo CC
Fotografía en Flick de senroy bajo CC
Fotografía en Flick de jackace bajo CC

Mira las curvas de las fotos. Otra de las características de las funciones es su curvatura, y los objetos que aparecen en las imágenes de arriba tienen diferente curvatura.

Si coges dos puntos de la parte superior del puente y los unes con una cuerda, esta quedará por debajo de la curva (es cóncavo). En el caso de la rampa, si unimos dos puntos la cuerda queda por encima (es convexa).

La curvatura de una función también se puede estudiar a partir de las derivadas. En la siguiente escena de geogebra, mueve el punto P a lo largo de la función para ver cómo varía la monotonía y la curvatura de la función.

Observa el cambio en la primera y segunda derivada en los puntos de abscisa x=-1, x=0, x=1, x=2 y x=3, e intenta averiguar la relación. Pulsando las casillas de monotonía y curvatura verás los intervalos en los que cambian estas dos características.

Importante

La curvatura de una función estudia la forma en que esa función se curva y se mide por su relación con la tangente. Hay dos tipos de curvatura.

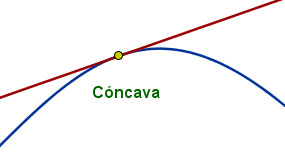
Una función se dice que es cóncava en un punto si al trazar la tangente a la función en dicho punto, la función queda por debajo de la tangente en los alrededores de ese punto.

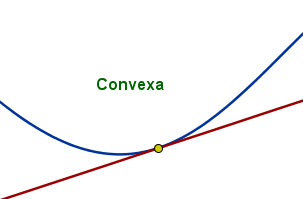
Una función se dice que es convexa en un punto si al trazar la tangente a la función en dicho punto, la función queda por encima de la tangente en los alrededores de ese punto.

Función cóncava Función convexa
Imágenes de elaboración propia

En el apartado 1 del tema hemos visto como el signo de la primera derivada nos indica la monotonía de una función. Ahora veremos como la curvatura viene determinada por el signo de la segunda derivada. Recorre la función de la siguiente ventana y observa el signo de la segunda derivada.


Aquí puedes ver tambien la escena de mduran bajo CC.

Importante

Si tenemos una función que admite, al menos, hasta la segunda derivada en un punto x=a tenemos el siguiente resultado.
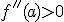  • Si f''(a)>0, la función es convexa (U) en el punto a.
  • Si 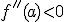f''(a)<0, la función es cóncava (∩) en x=a.
Luego para estudiar los intervalos de concavidad y convexidad de una función, basta estudiar donde es positiva y negativa la segunda derivada.

Caso de estudio

Estudia los intervalos de concavidad y convexidad de la función 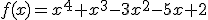f(x)=x^4+x^3-3x^2-5x+2

Reflexión

Plantas
Imagen en INTEF bajo CC

En un invernadero se está realizando el estudio del crecimiento de un nuevo tipo de planta. Es interesante estudiar cuando crece más y cuando menos, por ello, los científicos quieren estudiar la curvatura de la función que han aproximado al crecimiento de la planta en las primeras semanas. Esa función viene dada por la expresión

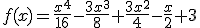
f(x) = \frac{x^4}{16} - \frac{3x^3}{8} + \frac{3x^2}{4} - \frac{x}{2} + 3

Ayúdales hallando los intervalos de concavidad y convexidad de esa función.

Importante

Punto de inflexión

Imagen de elaboración propia

Un punto de inflexión es aquel en el que la función cambia de curvatura, es decir, en el que pasa de cóncava a convexa o viceversa.

Si trazamos una tangente a la función en ese punto se puede apreciar que a un lado del punto la función queda por encima de la recta tangente y al otro lado por debajo.

Como en el punto de inflexión la función pasa de cóncava 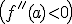\(f''(a)<0 \) a convexa 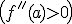\(f''(a)>0 \), lo normal es que en ese punto la función se anule. Compruébalo en la siguiente ventana observando que pasa en los puntos x=-3, x=0 y x=2, que son puntos de inflexión de la función.


Aquí puedes ver tambien la escena de mduran bajo CC.

Importante

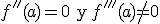Si una función f cumple en un punto x=a que f''(a)=0\begin{verbatim} y \end{verbatim}f'''(a) eq 0 entonces la función tiene en x=a un punto de inflexión.

Si es complicado el cálculo de la derivada tercera, lo usual es estudiar el signo de la segunda derivada antes y después del punto x=a. Si cambia su signo entonces es punto de inflexión.

Caso de estudio

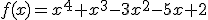
Determina los puntos de inflexión de la función f(x)=x^4+x^3-3x^2-5x+2

Actividad de rellenar huecos

Mandos compañía petrolera

Imagen en INTEF bajo CC

En una compañía petrolífera están estudiando el número de miles de bidones de combustible que han servido en las cuatro primeras semanas del mes. Les interesa conocer si el aumento o disminución ha sido muy rápido o no y para ello quieren localizar los puntos de inflexión en ese reparto.

Después del estudio realizado han aproximado la entrega de combustible a la función siguiente:

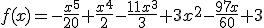
f(x)= - \frac{x^5}{20} + \frac{x^4}{2} - \frac{11x^3}{3} + 3x^2 - \frac{97x}{60} + 3
Los puntos de inflexión de esa función se obtienen en:

(1 , )

( , 7/2 )

( , )

Habilitar JavaScript

Observa el siguiente ejercicio resuelto por Saúl Valverde Pérez en donde se hace el estudio de la curvatura de una función.

AV - Actividad de Espacios en Blanco

Necesitamos estudiar la curvatura de la funciónf(x)=\frac{x^5+5x^4}{10} para un proyecto que estamos realizando. Completa los campos en blanco con los resultados que obtengas:

  • La primera derivada de la función es f '(x) = (x4+ x3) /
  • La segunda derivada es f ''(x) = x3+ x2
  • La función f(x) es cóncava en (-∞, )
  • La función f(x) es convexa en ( ,+∞)
  • Tiene un punto de inflexión en P=( , )
  • ¿Existe punto de inflexión en x=-3? (sí/no)

Habilitar JavaScript

Caso de estudio

Sea la función f: \ \mathbb{R} \rightarrow \mathbb{R} definida por 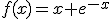f(x) = x + e^{-x}.
  1. Determina los intervalos de crecimiento y de decrecimiento de f, así como los extremos relativos o locales de f.
  1. Determina los intervalos de concavidad y convexidad de f.

Caso de estudio

Sea f: \ \mathbb{R} \rightarrow \mathbb{R} la función definida por 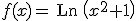f(x)=\begin{verbatim} Ln \end{verbatim}\(x^2+1\), siendo Ln la función logaritmo neperiano.

  1. Determina los intervalos de crecimiento y decrecimiento y los extremos relativos de la función f.
  1. Calcula la ecuación de la recta tangente a la gráfica de f en el punto de inflexión de abscisa negativa.

Reflexión

Sea f: \ \mathbb{R} \rightarrow \mathbb{R} la función definida por 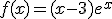f(x)=(x-3) e^x.
  1. Calcula los extremos relativos de f (puntos donde se obtienen y valores que se alcanzan).
  1. Determina la ecuación de la recta tangente a la gráfica de f en su punto de inflexión.