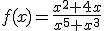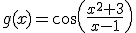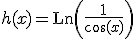2.2. Derivación de funciones compuestas. Regla de la cadena

Importante

Normalmente, las funciones que solemos encontrarnos no son funciones simples como las que vemos en la tabla de derivadas, sino que son funciones que se obtienen como composición de funciones simples.

Por ejemplo 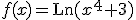f(x) = \begin{verbatim}Ln\end{verbatim} (x^4+3), en este caso vamos a aplicar lo que se conoce con el nombre de regla de la cadena.

Si llamamos 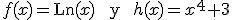f(x) = \begin{verbatim}Ln\end{verbatim} (x) \ \begin{verbatim} y \end{verbatim} \ h(x) = x^4+3 tenemos que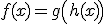 f(x) = g \left( h (x) \right)

La regla de la cadena nos dice quela derivada de una función compuesta es

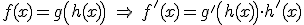
f(x) = g \left( h (x) \right) \ \Rightarrow \ f'(x) = g' \left( h (x) \right) \cdot h' (x)

 

En nuestro caso

f'(x) = \frac{1}{h (x)} \cdot 4x^3 = \frac{4x^3}{x^4+3}

 

Ponemos a tu disposición dos tablas de derivadas tabla 1, tabla 2. Ambas recogen tanto la derivación de las funciones elementales como las compuestas. Utiliza la que te resulte más cómoda. 

Reflexión

Ahora te toca practicar a tí. Para ello te proponemos que calcules la derivada de cada una de las siguientes funciones:

  1. f(x)=\frac{x^2+4x}{x^5+x^3} 
  1. g(x)=\cos \left( \frac{x^2+3}{x-1} \right) 

Caso de estudio

Aplica la regla de la cadena para obtener la función derivada de f(x) = ( 2x-1)^5

Una aplicación de la regla de la cadena para las funciones trigonométricas la observamos en el siguiente vídeo: 


En los siguientes enlaces puedes encontrar una relación de ejercicios de derivadas resueltos con los cuales puedes practicar.

 

 

Por último en el siguiente cuadro puedes observar un resumen de casi todo lo tratado a lo largo del tema. Pulsa sobre los botones que aparecen que te guiarán por el mismo:

Animación en wikispaces de Salvador Hurtado bajo CC