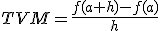1.1. Tasa de variación media y variación instantánea

Importante

Si tenemos una función f, la tasa de variación media de la función entre dos puntos a y b viene dada por:

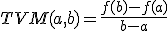
TVM(a,b)=\frac{f(b)-f(a)}{b-a}

Geométricamente, la tasa de variación media de la función f en el intervalo [a,b] es la pendiente de la recta secante a la gráfica de f que pasa por los puntos (a,f(a)) y (b,f(b)).

Observemos la siguiente escena de GeoGebra. En ella, podemos calcular distintas TVM para la función f(x)=x2+2x en cualquier intervalo y ver qué relación guarda con la recta secante.

 

Caso de estudio

Calcula la tasa de variación media de la función f(x)=x2+3x+1 en el intervalo [-2,1]

Si ahora volvemos a las funciones y, teniendo en cuenta que b es mayor que a, se puede expresar b como a+h, donde h sería un número real y positivo, y de esta forma la tasa de variación media se podría expresar con la siguiente fórmula:

TVM=\frac{f(a+h)-f(a)}{h}

 

 

Si h se aproxima a cero, el punto b=a+h se aproximará al punto a y la tasa de variación media tenderá entonces a un valor que denominamos tasa de variación instantánea de la función f en el punto a. Que si hablamos en términos de velocidad, sería justo la que marca el velocímetro de nuestro coche en un determinado momento.

Importante

La tasa de variación instantánea de una función f en un punto viene dada por:

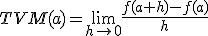
TVM(a) = \lim_{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}

Caso de estudio

Calcula la tasa de variación instantánea de la función f(x)=x2 en x=2

Actividad de rellenar huecos

Unos diseñadores informáticos han estado trabajando durante varios meses para poder acercar, a través de Internet, una visita a la Capilla Sixtina.  El movimiento que se puede realizar en cada una de las direcciones dentro de la recreación virtual de la Capilla, lo han conseguido a través de una función plana que se aplica en la dirección en la que se mueve el ratón del ordenador, de forma que pueda seguir ofreciendo una perspectiva próxima a la realidad. La función utilizada es:

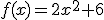
f(x)=2x^2+6

De esta función han realizado las siguientes anotaciones en su estudio:

1.- La tasa de variación media entre los valores 1 y 3 es .

2.- La tasa de variación media entre los valores 4 y 8 es .

3.- La tasa de variación instantánea en el valor 3 es .

4.- La tasa de variación instantánea en el valor 5 es .

Ayúdales completando los valores.

Habilitar JavaScript

Caso de estudio

Fórmula I

Fotografía en Flick de williamcho bajo CC

La empresa de motores MOTORESA ha diseñado un nuevo motor de gasolina que pretende introducir en el mercado. Los ingenieros de la empresa saben que el consumo de gasolina depende de la velocidad a la que vaya el motor. Si llamamos a la velocidad, la función que proporciona el consumo de gasolina en función de la velocidad es

Para contrastar lo bueno que es el motor frente a sus competidores, han decidido basarse en la tasa de variación instantánea del consumo del motor a velocidad 1.

Calcula esa tasa de variación instantánea.