3. Extremos (máximos y mínimos)
Estamos acostumbrados a oír hablar de temperaturas máximas y mínimas todos los días en las noticias. De hecho, es una frase muy habitual la de "se ha alcanzado una máxima de 40º de temperatura". En la siguiente gráfica, de la AEMET, en la que podemos ver la temperatura que ha hecho en Málaga desde las 19h del 13 de abril a las 18h del día siguiente. Puedes comprobar que:
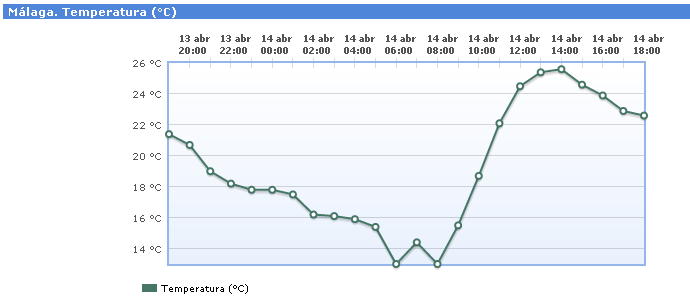
- La temperatura máxima se alcanza a las 14h del 14 de abril (25,6ºC)
- La temperatura mínima se alcanza a las 6h y a las 8h del 14 de abril (13ºC)
- A las 7h del 14 de abril hay un máximo relativo, pues es la temperatura más alta en un pequeño periodo de tiempo (de las 6 a las 8h).
Para poder averiguar la temperatura máxima o mínima necesitamos una tabla de datos observados o una gráfica como la anterior, pues la temperatura local no la podemos expresar con una función derivable.
Veamos por tanto qué ocurre en la siguiente función, y comparemos con su derivada:
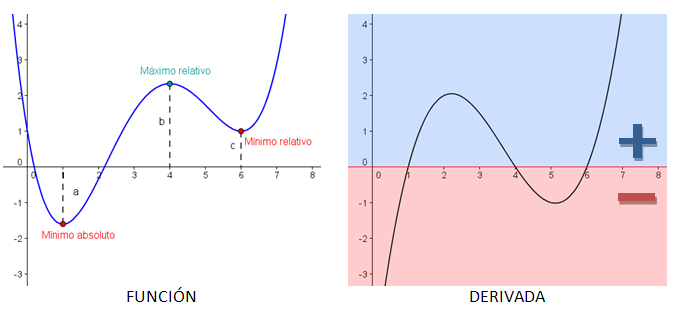
A la izquierda tenemos una función f(x) y a la derecha su derivada f '(x).
- Mínimo: si te fijas en los dos mínimos, a su izquierda la función es decreciente y a la derecha es creciente ¿qué quiere decir eso para la derivada? Como vimos en el apartado anterior, equivale a que a la izquierda la derivada es negativa y a la derecha positiva (como puedes ver en la gráfica de la derivada). Pues si en ese punto la derivada pasa de negativa a positiva, quiere decir que debe ser nula.
- Máximo: en el máximo pasa algo parecido, pero en este caso pasamos de función creciente a decreciente, es decir, de derivada positiva a negativa. Al igual que antes, en ese punto la derivada debe ser nula.
Importante
Imagen de elaboración propia
|
Si una función tiene un extremo relativo en el punto x=a y, en él, existe la derivada, entonces se cumple que f'(x)=0.
Los puntos que anulan la primera derivada reciben el nombre de puntos críticos y, entre ellos, pueden estar los extremos relativos de una función.
El problema se plantea en que no siempre se cumple lo contrario de lo que aparece anteriormente. Una función puede anular su derivada en un punto y sin embargo no tener en él un extremo relativo. Por ejemplo, la función f(x)=x3 siempre es creciente, mientras mayor es x mayor es la función, por tanto, no tiene extremos. Sin embargo, su derivada en el punto x=0 vale cero. Por ello vamos a ampliar las condiciones anteriores con nuevos datos.
Importante
Si la función f(x) tiene derivada nula en el punto x=a, f'(a)=0, y existe la segunda derivada en dicho punto se cumple:
- Si f''(a)<0, la función tiene (o alcanza) un máximo relativo en x=a.
- Si f''(a)>0, la función tiene (o alcanza) un mínimo relativo en x=a.
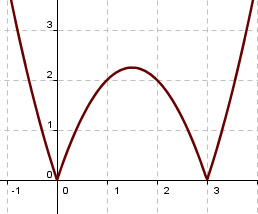
Imagen de elaboración propia
|
Como puedes observar seguimos dejándonos casos atrás, porque en lo anterior no se dice nada sobre qué ocurre si f''(a)=0. Además puede haber funciones que tengan extremos relativos y su derivada primera no se anule porque no exista la derivada de la función en ese punto. Por ejemplo, eso le ocurre a la función f(x)=|x2-3x| en los puntos en los que tiene mínimos relativos, como puedes apreciar en la imagen.
Por ello, en general, lo más cómodo es estudiar el signo de la primera derivada (en aquellos puntos en los que exista) y tener presente las siguientes definiciones:
- Una función alcanza un máximo relativo en un punto si en él pasa de ser creciente a decreciente.
- Una función alcanza un mínimo relativo en un punto si en él pasa de ser decreciente a creciente.
Curiosidad
Como la derivada de una función en un punto también representa la pendiente de la recta tangente a la función en ese punto, la monotonía y los extremos de una función se pueden explicar a partir de la pendiente de la recta tangente. Si quieres saber más, visita la web de Manuel Sada.
Para que veas cómo podemos hallar máximos y mínimos con la derivada, mira el siguiente ejercicio resuelto.
AV - Pregunta de Selección Múltiple
Solution
Solution
Solution
Solution
Caso de estudio
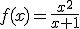
Actividad de rellenar huecos
Ejemplo o ejercicio resuelto
La potencia f(x) en vatios consumida por cierto aparato eléctrico, en función de su resistencia (x) en ohmios viene dada por la expresión:
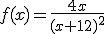
|
Hallar la potencia máxima y el correspondiente valor de x.
Ejemplo o ejercicio resuelto
Prueba de Acceso a Grados para Mayores de 25 años - Año 2007
Halle los máximos y mínimos relativos de la función f(x)=x3-9x. Determine también en qué intervalos es creciente y decreciente la función.
Caso de estudio
Sea 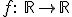 la función definida por
la función definida por 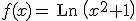 , siendo Ln la función logaritmo neperiano.
, siendo Ln la función logaritmo neperiano.
- Determina los intervalos de crecimiento y decrecimiento y los extremos relativos de la función f.
- Calcula la ecuación de la recta tangente a la gráfica de f en el punto de inflexión de abscisa negativa.
Reflexión
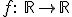 la función definida por
la función definida por 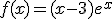 .
.
- Calcula los extremos relativos de f (puntos donde se obtienen y valores que se alcanzan).
- Determina la ecuación de la recta tangente a la gráfica de f en su punto de inflexión.
