6. Variables aleatorias continuas
Importante

|
Pensando en la prueba...
Las actividades sobre cálculo de probabilidades con variables aleatorias que se distribuyen según una normal son muy frecuentes en la prueba, por eso junto con el examen siempre viene adjunta la tabla necesaria para ello. Por este motivo es imprescindible:
- Saber calcular probabilidades con la normal estándar
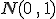 .
. - Calcular probabilidades distintas de las que te da directamente la tabla, ya sea tipificando una normal de media
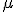 y desviación típica
y desviación típica 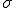 , recurriendo al contrario...
, recurriendo al contrario...
Importante
Una variable aleatoria continua 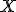 queda determinada por una función f que llamaremos función de probabilidad o función de densidad.
queda determinada por una función f que llamaremos función de probabilidad o función de densidad.
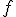 debe ser siempre mayor o igual que cero y el área debajo de su gráfica tiene que ser 1.
debe ser siempre mayor o igual que cero y el área debajo de su gráfica tiene que ser 1.
La probabilidad estará definida como el área delimitada por la gráfica de 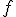 y el eje horizontal.
y el eje horizontal.
En el caso de 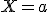 , dicha probabilidad es cero
, dicha probabilidad es cero 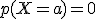 , ya que no se encierra ningún área.
, ya que no se encierra ningún área.
Para un intervalo, la 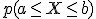 será igual al área que hay bajo la gráfica de
será igual al área que hay bajo la gráfica de 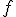 en el intervalo
en el intervalo 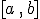 .
.
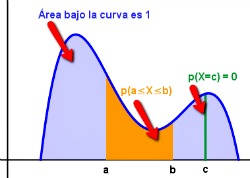
Imagen de elaboración propia
|
Del mismo modo que entre las variables discretas hemos introducido el modelo binomial, entre las variables continuas vamos a introducir un modelo al que se ajusta un gran número de variables de nuestro entorno. Este modelo se va a llamar distribución Normal, y su nombre se debe ni más ni menos a que la gran mayoría de variables que se refieren a aspectos físicos, psicológicos, sociológicos, biológicos, etc. se ajustan a este modelo, o sea, que lo normal, es que sea una variable Normal.
La distribución Normal se expresa por 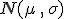 , donde el primer parámetro
, donde el primer parámetro 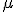 , representa la media de la variable aleatoria y
, representa la media de la variable aleatoria y 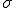 la desviación típica, y la representación de su función de densidad es una campana de Gauss:
la desviación típica, y la representación de su función de densidad es una campana de Gauss:
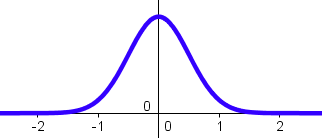
|
En el caso particular de que la sea media 0 y desviación típica 1, es decir, 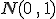 , la llamamos distribución Normal estándar y la designamos por
, la llamamos distribución Normal estándar y la designamos por 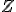 .
.
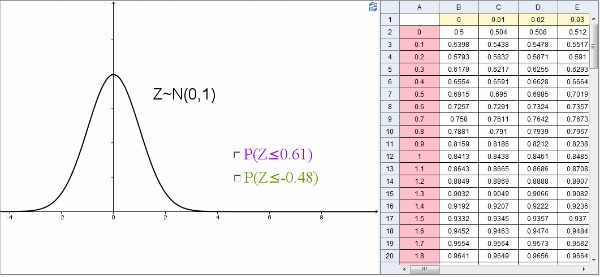
Esta distribución Normal estándar la utilizaremos para calcular probabilidades de variables aleatorias que se distribuyen según una Normal, independientemente de su media y su desviación. Pero antes de dar este paso hay que saber cómo calcular las probabilidades asociadas a esa Normal estándar, para lo que utilizaremos una tabla donde se recoge 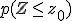 con
con 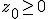 , que es el área encerrada debajo de la campana de Gauss para valores inferiores a
, que es el área encerrada debajo de la campana de Gauss para valores inferiores a 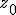 :
:
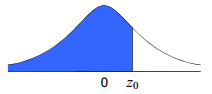
|
La siguiente presentación te será muy útil para aprender el manejo de dicha tabla:
Resumiendo para calcular la  con
con 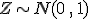 y
y 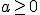 , solo debemos acudir a la tabla. Pero, ¿qué ocurre cuando aún distribuyéndose según una
, solo debemos acudir a la tabla. Pero, ¿qué ocurre cuando aún distribuyéndose según una 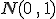 queremos averiguar
queremos averiguar 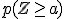 o
o 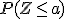 con
con 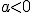 , incluso la combinación de ambas cosas?
, incluso la combinación de ambas cosas?
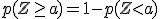 |
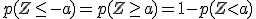 |
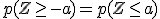 |
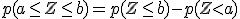 |
Para memorizar estas "fórmulas" solo tienes que racionalizarlas, recurriendo a su interpretación geométrica. A esto te puede ayudar la siguiente escena de Geogebra que además está acompañada de la tabla de la distribución normal, para que contrastes los resultados.
Por último, en el caso en el que no trabajemos con la Normal estándar, sino que nos den una media 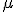 distinta de 0 o una desviación típica
distinta de 0 o una desviación típica 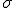 distinta de 1, tendremos que recurrir a la tipificación de la variable
distinta de 1, tendremos que recurrir a la tipificación de la variable 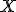 . Este proceso consistirá en convertir una variable
. Este proceso consistirá en convertir una variable 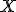 que se distribuye según una Normal
que se distribuye según una Normal 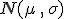 en una Normal estándar
en una Normal estándar 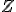 , para lo que restaremos
, para lo que restaremos 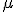 a la variable
a la variable 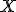 y dividiremos entre
y dividiremos entre 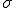 , esto es:
, esto es:
Si ![]() entonces
entonces ![]() .
.
Puedes practicar este proceso con las siguientes actividades de pruebas anteriores:
Caso de estudio

|
Curso 2009/2010
En un colegio se estudia la distribución de la nota de Matemáticas de sus estudiantes, resultando ser una Normal de media 7.2 y desviación típica 1.2. Se elige al azar un estudiante de ese colegio, ¿cuál será la probabilidad de que su nota en esta asignatura sea mayor que 7.5?
Caso de estudio

|
Curso 2010/2011
El peso de las manzanas que se producen en una huerta sigue una ley Normal con una media de 150 gramos y desviación típica de 20 gramos.
a) ¿Qué porcentaje de estas manzanas tendrá un peso inferior a 115 gramos?
b) Halla la probabilidad de que una manzana, elegida al azar en este huerto, tenga un peso que se encuentre entre 165 y 220 gramos?
Caso de estudio

|
Curso 2011/2012
La duración de un tipo de pilas alcalinas sigue una distribución Normal de media 55 horas y una desviación típica de 6 horas.
a) Calcula la probabilidad de que una pila elegida al azar dure más de 53 horas.
b) Halla la probabilidad de que una pila elegida al azar dure entre 56 y 58 horas.