2. Estadística unidimensional
Importante

|
Pensando en la prueba...
Lo más importante de la estadística unidimensional, en relación con el examen de la PAU para mayores de 25 años y en función de las pruebas aparecidas en años anteriores, es saber organizar la información en tablas de frecuencias, y calcular los parámetros de centralización (media y moda) y los de dispersión (varianza y desviación típica). Esto requiere ser meticuloso en los cálculos, ya que un simple error al obtener la frecuencia, la marca de clase, incluso en la media puede provocar que el resto de la actividad no sea correcta.
La Estadística es la rama de las matemáticas que se encarga de recolectar y organizar datos con el objeto de inferir conclusiones sobre ellos. Al igual que en Álgebra, hablábamos de ecuaciones, incógnitas..., la Estadística tiene su propio vocabulario para referirse a los distintos elementos que componen un estudio estadístico. En la siguiente presentación puedes repasar los más comunes:
Cuando realizamos un estudio estadístico, los datos que obtenemos debemos organizarlos para poder sacar conclusiones provechosas de ellos. Tenemos dos formas de organizar estos datos: mediante tablas o/y gráficos estadísticos. En la siguiente presentación te explicamos cómo recoger toda la información en una tabla que posteriormente te será muy útil. Además, con relación a los gráficos estadísticos destacamos dos, por su sencillez de construcción y por la información que nos trasladan a simple vista.
Importante
Notación
Muchos de los conceptos mencionados anteriormente los denotamos con una nomenclatura especial.
| Marca de clase o datos |
Número |
Frecuencia absoluta |
Frecuencia relativa |
Frecuencia abs. |
Frecuencia rel. |
| xi |
N |
ni |
fi |
Ni |
Fi |
Puede ocurrir que si utilizas otros textos como referencia, esta notación cambie.
Por último, para analizar estos datos se hace imprescindible resumirlos de manera que se conserve la mayor información posible y que representen el comportamiento global de la población.
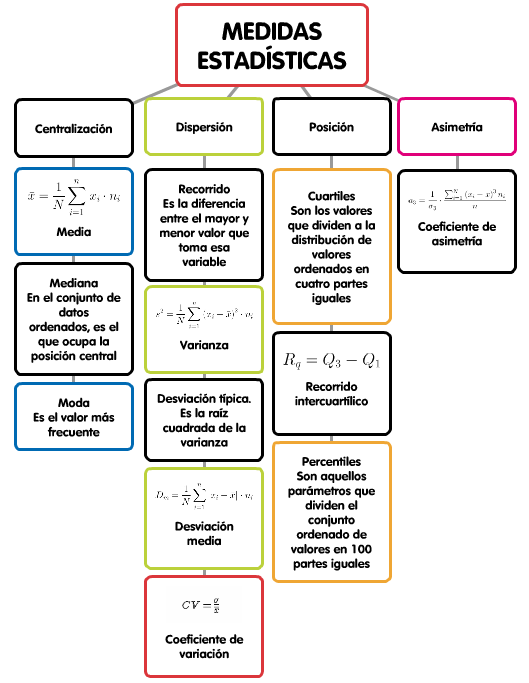
Esto lo vamos a hacer a través de una serie de medidas que complementarán unas a otras:
- Medidas de centralización, buscan las características del centro de la distribución, y son la media, moda y mediana.
- Medidas de posición, indican, una vez ordenados, cuántos elementos quedan a la izquierda o derecha de uno dado: cuartiles, deciles, centiles o percentiles.
- Medidas de dispersión, proporcionan una idea sobre la separación de los datos: rango o recorrido, desviación media, varianza, desviación típica y coeficiente de variación.
- Medidas de forma, proporcionan una idea de la simetría de la distribución: coeficiente de asimetría.
Caso de estudio

|
Curso 2011/2012
En una urbanización se ha realizado un estudio sobre el número de personas que habitan en cada piso y se obtienen los siguientes datos:
| Personas | 1 | 2 | 3 | 4 | 5 |
| Pisos | 20 |
60 |
52 | 35 |
18 |
a) ¿Cuántos pisos hay en la urbanización?
b) Determine la media y la moda de la distribución.
c) Determine la varianza y la desviación típica de la misma.
Caso de estudio

|
Curso 2010/2011
En la corrección de errores tipográficos de un texto se han encontrado 22 páginas con un solo error en cada una, 9 páginas con dos errores en cada una, 6 páginas con 3 errores en cada una, 3 páginas con 4 errores en cada una, 2 páginas con 5 errores en cada una y ningún error en las 58 páginas restantes.
a) Construya las tablas de frecuencias absolutas y relativas de la distribución del número de errores por página de ese texto.
b) Halle la media y la desviación típica del número de errores por página de dicho texto.